- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многослойные сети. Алгоритмы обучения презентация
Содержание
- 1. Многослойные сети. Алгоритмы обучения
- 2. Структура многослойных сетей 1. Сети с прямой
- 3. Многослойные сети Особенности: 1. Нейроны выходного слоя
- 4. Алгоритмы обучения Классификация алгоритмов По математическому
- 5. Алгоритмы обучения сетей с прямой передачей сигнала Обобщенное Дельта-правило где
- 6. Алгоритмы локальной оптимизации с вычислением частных производных
- 7. Стохастические методы обучения В основе работы –
- 8. Методы глобальной оптимизации Решение задачи глобальной оптимизации
- 9. Метод обратного распространения ошибки (error back-propagation) Применяется
- 10. Метод обратного распространения ошибки (error back-propagation) Производная
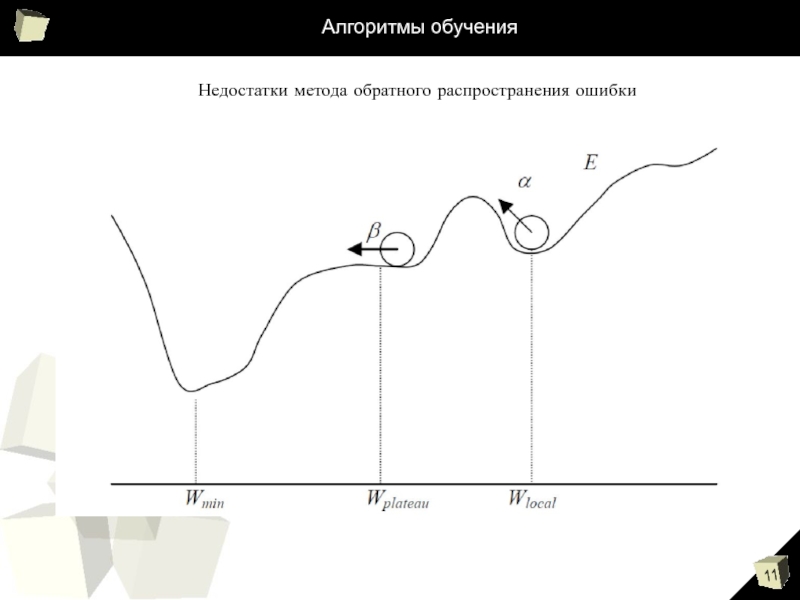
- 11. Алгоритмы обучения Недостатки метода обратного распространения ошибки
- 12. Некоторые алгоритмы неконтролируемого обучения 1. Правило Хебба.
- 13. Алгоритм обучения Хебба i-й нейрон
- 14. Алгоритм конкурентного обучения Кохонена Нейрон-победитель Нормализация вектора весовых коэффициентов: Коррекция вектора весовых коэффициентов:
- 15. Геометрическая интерпретация алгоритма Кохонена Победителем объявляется нейрон,
- 16. Сети Кохонена с самоорганизующейся структурой Сеть с
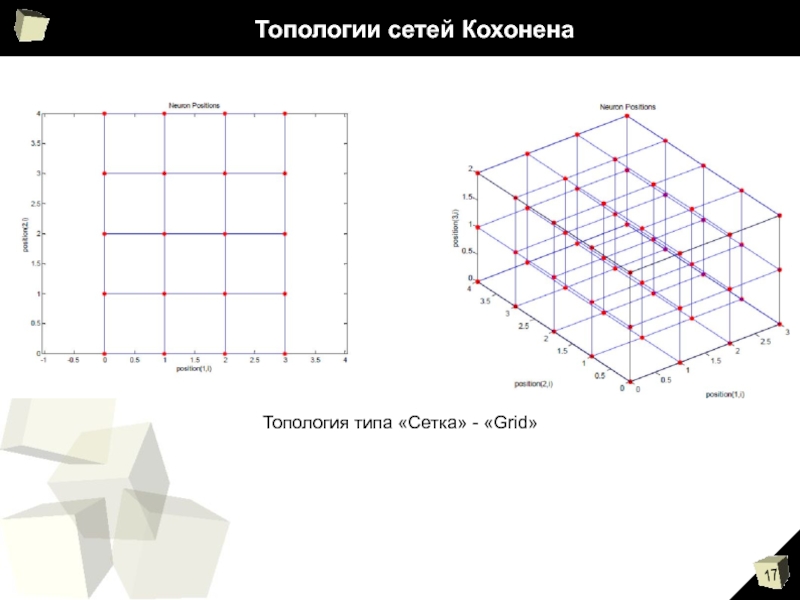
- 17. Топологии сетей Кохонена Топология типа «Сетка» - «Grid»
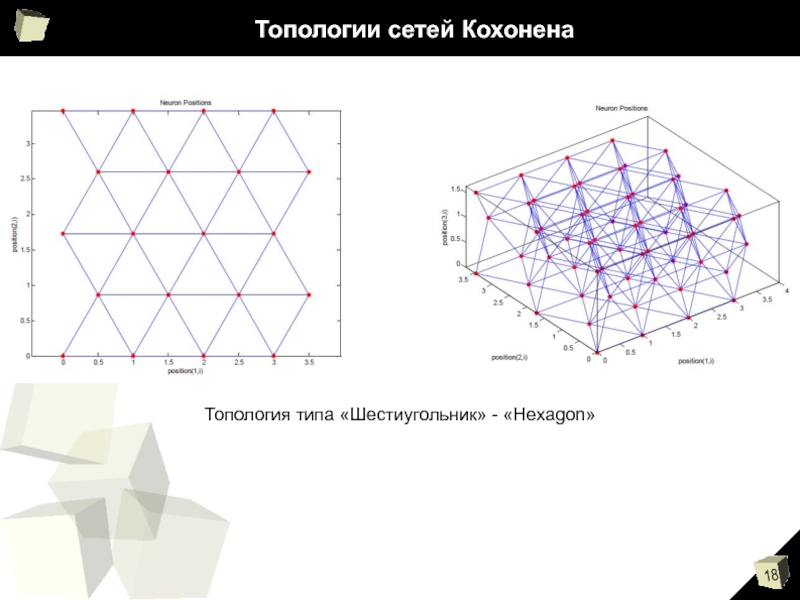
- 18. Топологии сетей Кохонена Топология типа «Шестиугольник» - «Hexagon»
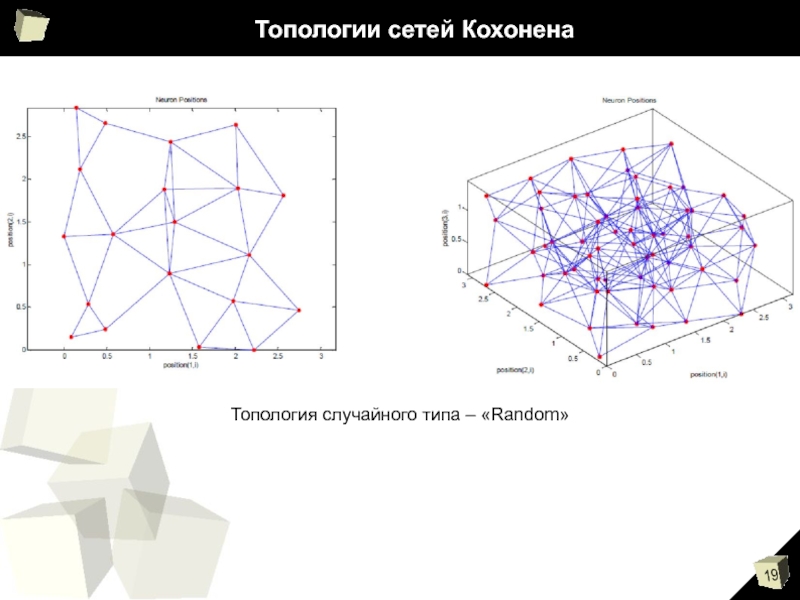
- 19. Топологии сетей Кохонена Топология случайного типа – «Random»
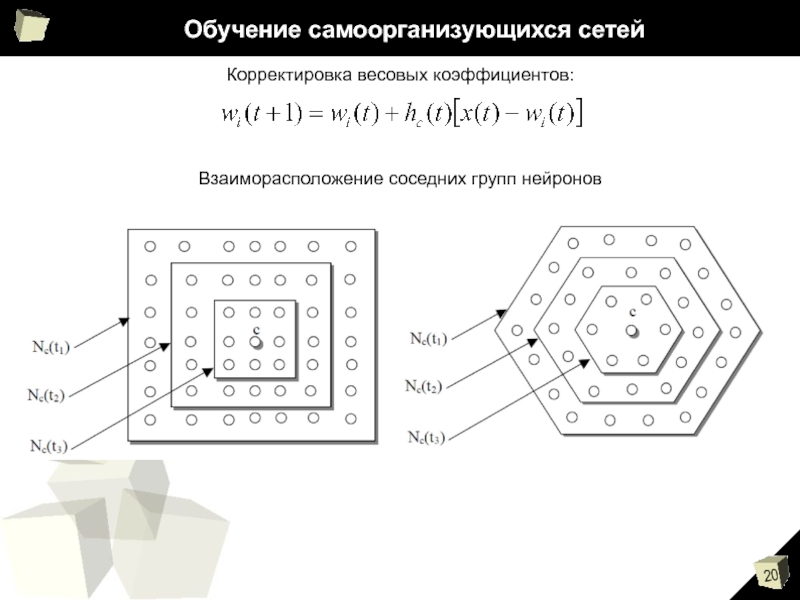
- 20. Обучение самоорганизующихся сетей Корректировка весовых коэффициентов: Взаиморасположение соседних групп нейронов
- 21. Процесс обучения сетей Кохонена
Слайд 1Курс «Нейронные сети и системы нечеткой логики»
Лекция 2
Многослойные сети. Алгоритмы обучения.
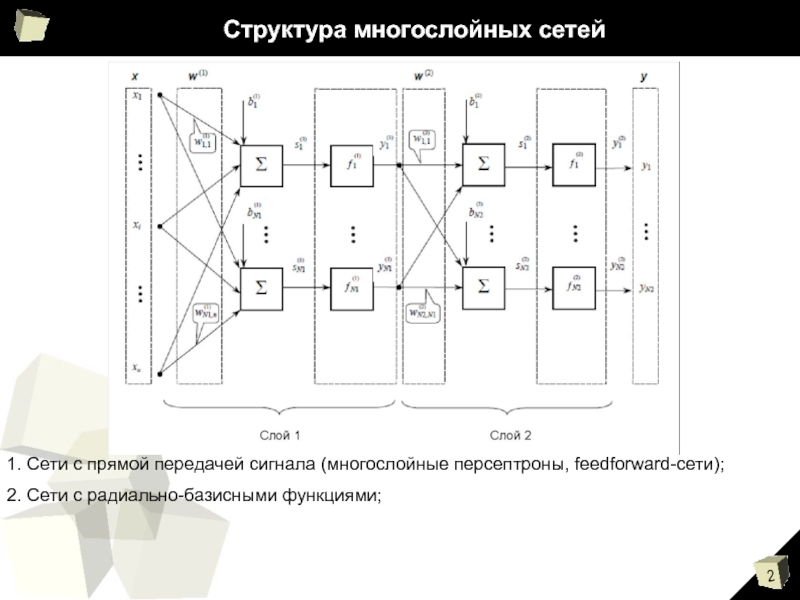
Слайд 2Структура многослойных сетей
1. Сети с прямой передачей сигнала (многослойные персептроны, feedforward-сети);
2.
Сети с радиально-базисными функциями;
Слайд 3Многослойные сети
Особенности:
1. Нейроны выходного слоя обычно имеют линейную функцию активации;
2. Принцип
работы существенно зависит от выбранной функции активации скрытых нейронов;
3. Наиболее часто используемая структура сети;
Преимущества:
1. Принцип работы легко описывается матричными уравнениями;
2. Универсальный аппроксиматор/классификатор;
Недостатки:
1. Сложные алгоритмы обучения;
2. Отсутствие точной методики выбора количества слоев и нейронов в них;
3. Наиболее часто используемая структура сети;
Преимущества:
1. Принцип работы легко описывается матричными уравнениями;
2. Универсальный аппроксиматор/классификатор;
Недостатки:
1. Сложные алгоритмы обучения;
2. Отсутствие точной методики выбора количества слоев и нейронов в них;
Слайд 4Алгоритмы обучения
Классификация алгоритмов
По математическому аппарату:
1. Алгоритмы локальной оптимизации с вычислением частных
производных первого порядка;
2. Алгоритмы локальной оптимизации с вычислением частных производных первого и второго порядка;
3. Стохастические алгоритмы оптимизации;
4. Глобальные методы оптимизации.
По наличию эталонного сигнала
1. Контролируемое обучение.
2. Неконтролируемое обучение (без учителя).
2. Алгоритмы локальной оптимизации с вычислением частных производных первого и второго порядка;
3. Стохастические алгоритмы оптимизации;
4. Глобальные методы оптимизации.
По наличию эталонного сигнала
1. Контролируемое обучение.
2. Неконтролируемое обучение (без учителя).
Слайд 6Алгоритмы локальной оптимизации с вычислением частных производных
Принцип работы основывается на поиске
градиента функции ошибки – направления наибольшего возрастания или убывания функции:
Где R – матрица поиска направления движения, λ – величина шага.
Варианты:
1. Метод градиентного спуска;
2. Метод сопряженного градиента;
3. Метод антиградиента.
Методы первого порядка вычисляют матрицу направления как:
Методы второго порядка:
Где Н – матрица Гессе частных производных критерия обучения по весовым коэффициентам
Где R – матрица поиска направления движения, λ – величина шага.
Варианты:
1. Метод градиентного спуска;
2. Метод сопряженного градиента;
3. Метод антиградиента.
Методы первого порядка вычисляют матрицу направления как:
Методы второго порядка:
Где Н – матрица Гессе частных производных критерия обучения по весовым коэффициентам
Слайд 7Стохастические методы обучения
В основе работы – поиск и обход локальных минимумов
функции ошибки по принципу «проб и ошибок».
Варианты:
1. Машины Больцманна;
2. Метод Монте-Карло и др.
Случайный характер изменения направления поиска увеличивает затраты времени на обучение сетей. Такой алгоритм применяется редко в чистом виде.
Использование генетических алгоритмов позволяет ускорить поиск и обход локальных минимумов за счет случайных «мутаций».
Варианты:
1. Машины Больцманна;
2. Метод Монте-Карло и др.
Случайный характер изменения направления поиска увеличивает затраты времени на обучение сетей. Такой алгоритм применяется редко в чистом виде.
Использование генетических алгоритмов позволяет ускорить поиск и обход локальных минимумов за счет случайных «мутаций».
Слайд 8Методы глобальной оптимизации
Решение задачи глобальной оптимизации состоит в систематическом переборе значений
всех аргументов.
Данный метод применяется только для сетей с простой структурой, поскольку сложность математических расчетов существенно возрастает с увеличением размерности решаемой задачи.
Данный метод применяется только для сетей с простой структурой, поскольку сложность математических расчетов существенно возрастает с увеличением размерности решаемой задачи.
Слайд 9Метод обратного распространения ошибки (error back-propagation)
Применяется только для сетей с прямой
(последовательной передачей сигнала), что обусловило устоявшееся обозначение таких сетей как feedforward-backpropagation networks. Этот метод относится к градиентным алгоритмам локальной оптимизации.
Суть метода заключается в передаче сигнала ошибки с выходного нейрона на нейроны скрытого слоя, на основании чего рассчитываются корректировки весовых коэффициентов.
За счет применения последовательной коррекции весовых коэффициентов существенно облегчается процедура нахождения направления движения.
Если представить сеть в виде цепочки матричных уравнений:
То можно получить:
Суть метода заключается в передаче сигнала ошибки с выходного нейрона на нейроны скрытого слоя, на основании чего рассчитываются корректировки весовых коэффициентов.
За счет применения последовательной коррекции весовых коэффициентов существенно облегчается процедура нахождения направления движения.
Если представить сеть в виде цепочки матричных уравнений:
То можно получить:
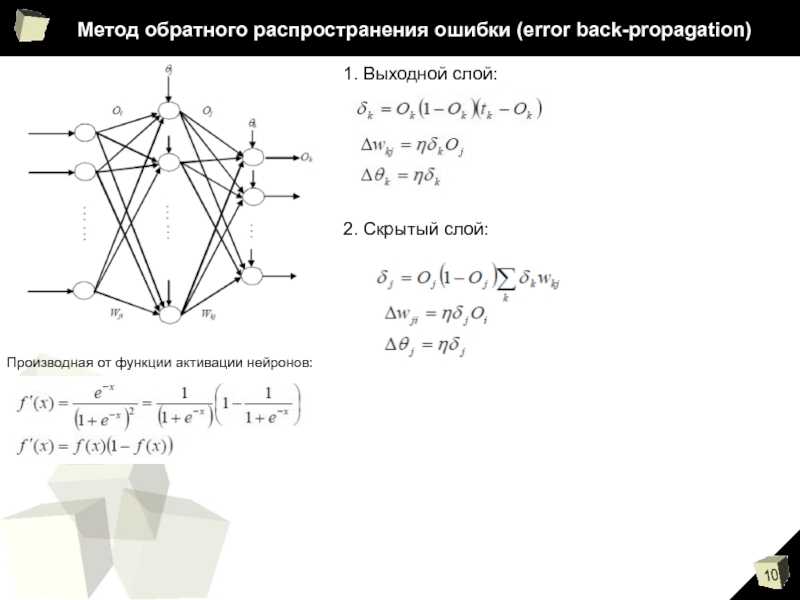
Слайд 10Метод обратного распространения ошибки (error back-propagation)
Производная от функции активации нейронов:
1. Выходной
слой:
2. Скрытый слой:
2. Скрытый слой:
Слайд 12Некоторые алгоритмы неконтролируемого обучения
1. Правило Хебба.
Если нейрон получает на вход сигнал
другого нейрона и они оба являются активными, то есть, имеют одинаковый знак, то весовой коэффициент связи этих нейронов необходимо усилить.
2. Правило Хопфилда.
Если входной и выходной сигнал одновременно активны или неактивны, весовой коэффициент связи этих сигналов необходимо увеличить на величину коэффициента обучения, в противном случае его необходимо уменьшить на эту же величину.
3. Правило Кохонена (победитель получает все).
На выход нейронной сети подается выходной сигнал нейрона с наибольшим значением выходного сигнала (победителя). Корректировка весовых коэффициентов осуществляется только для этого нейрона и нейронов из некоторой окрестности в структуре нейронной сети.
2. Правило Хопфилда.
Если входной и выходной сигнал одновременно активны или неактивны, весовой коэффициент связи этих сигналов необходимо увеличить на величину коэффициента обучения, в противном случае его необходимо уменьшить на эту же величину.
3. Правило Кохонена (победитель получает все).
На выход нейронной сети подается выходной сигнал нейрона с наибольшим значением выходного сигнала (победителя). Корректировка весовых коэффициентов осуществляется только для этого нейрона и нейронов из некоторой окрестности в структуре нейронной сети.
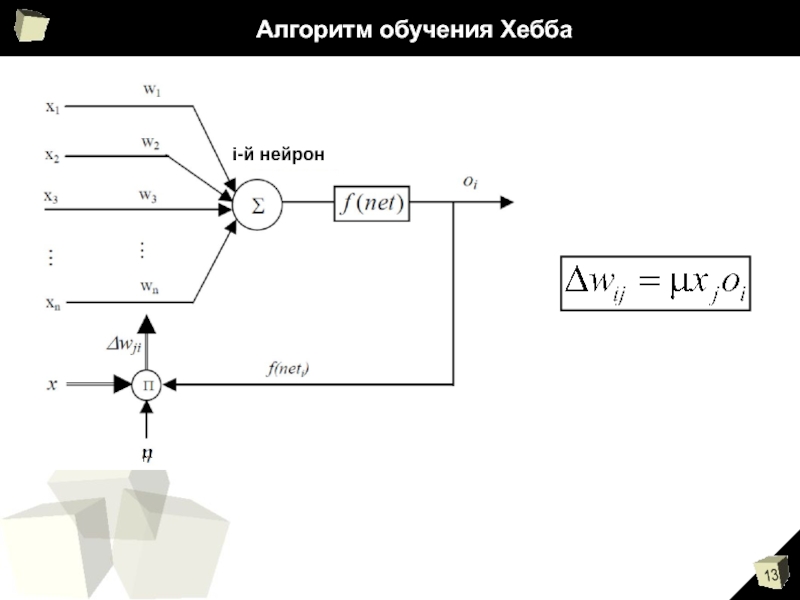
Слайд 14Алгоритм конкурентного обучения Кохонена
Нейрон-победитель
Нормализация вектора весовых коэффициентов:
Коррекция вектора весовых коэффициентов:
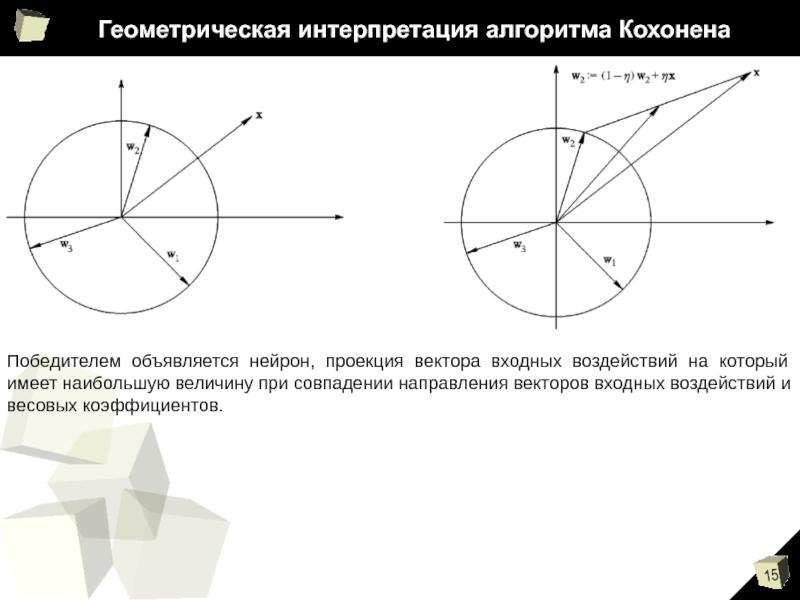
Слайд 15Геометрическая интерпретация алгоритма Кохонена
Победителем объявляется нейрон, проекция вектора входных воздействий на
который имеет наибольшую величину при совпадении направления векторов входных воздействий и весовых коэффициентов.
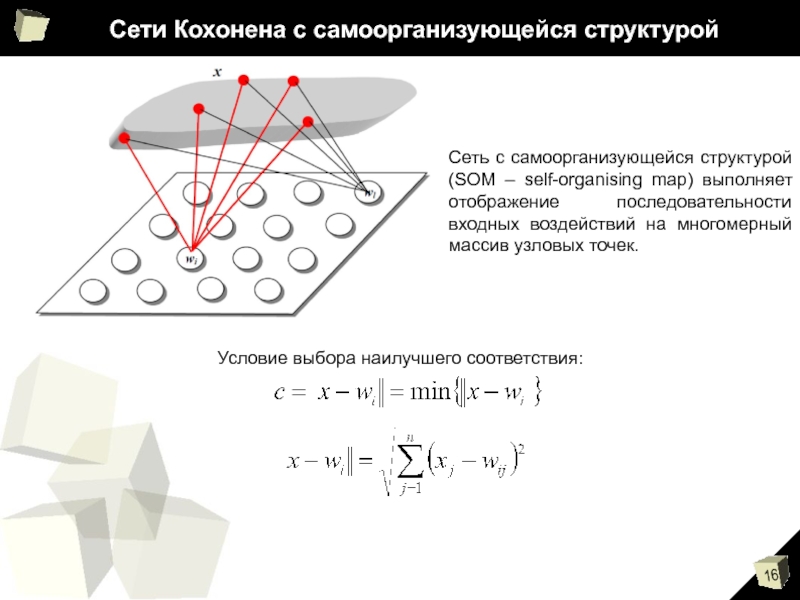
Слайд 16Сети Кохонена с самоорганизующейся структурой
Сеть с самоорганизующейся структурой (SOM – self-organising
map) выполняет отображение последовательности входных воздействий на многомерный массив узловых точек.
Условие выбора наилучшего соответствия: