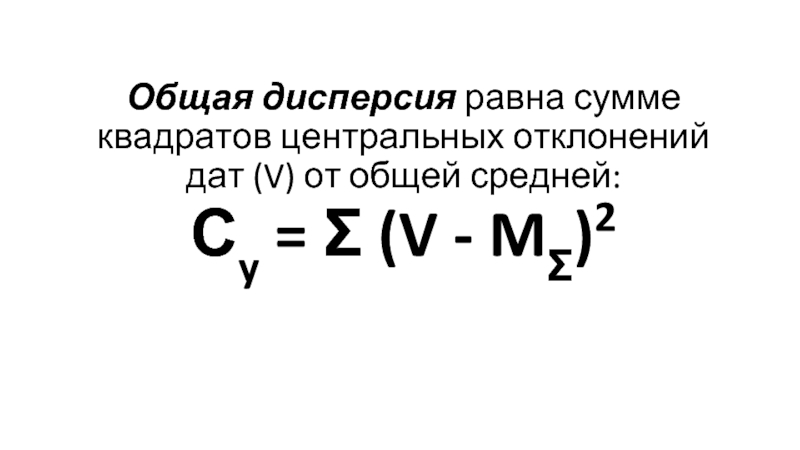- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дисперсионный анализ презентация
Содержание
- 1. Дисперсионный анализ
- 2. Возможности дисперсионного анализа: 1. Оценка силы и
- 3. Результативный признак – признак, изменяющийся под влиянием
- 4. Типы дисперсионных комплексов: • Однофакторные; • Двух-, трех- и
- 5. Dy=Dx+De, где Dx – межгрупповая дисперсия,
- 6. 1. Факториальная (межгрупповая) дисперсия равна сумме взвешенных квадратов
- 7. Случайная дисперсия (внутригрупповая) равна сумме квадратов центральных
- 8. Общая дисперсия равна сумме квадратов центральных отклонений
- 10. Закон аддитивности: в любом дисперсионном комплексе
- 11. Основной показатель силы влияния
- 12. Эмпирический критерий достоверности силы влияния
- 13. Ошибка репрезентативности
- 14. Фактически полученное дисперсионное отношение является величиной случайной,
- 15. На учебно-опытном участке агростанции изучали влияние различных
Слайд 2Возможности дисперсионного анализа: 1. Оценка силы и достоверности влияний. 2. Оценка разности частных средних
и частных долей.
3. Оценка наследуемости признаков в определенных группах особей при передаче генетической информации из поколения в поколение.
4. Анализ комбинационной способности ♀ и ♂ линий.
Слайд 3 Результативный признак – признак, изменяющийся под влиянием различных причин X, Y,
Z.
Факторы, вызывающие изменение признака, обозначаются А, В, С.
Организованные (регулируемые) факторы – испытывают серийно, в виде нескольких независимых друг от друга доз (градаций).
Слайд 4Типы дисперсионных комплексов:
• Однофакторные;
• Двух-, трех- и многофакторные;
• Равномерные, пропорциональные – ортогональные;
• Неравномерные – неортогональные.
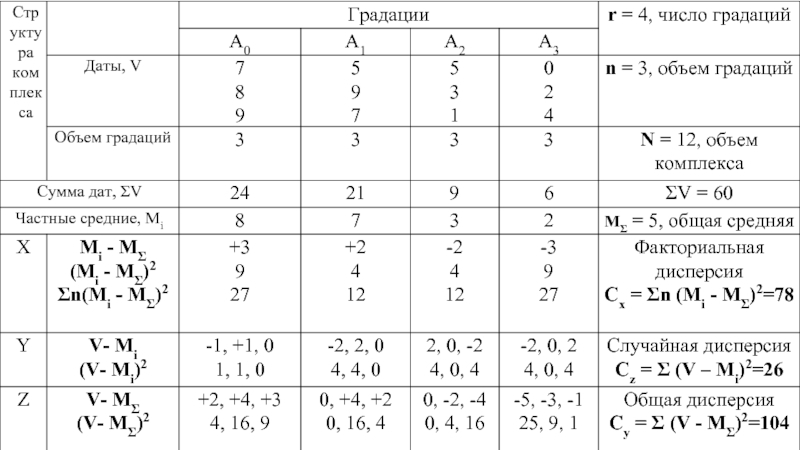
Слайд 5Dy=Dx+De, где Dx – межгрупповая дисперсия, представляющая собой сумму квадратов отклонений
групповых средних от общей средней комплекса, взвешенную на численность вариант в группах n.
Слайд 61. Факториальная (межгрупповая) дисперсия равна сумме взвешенных квадратов центральных отклонений частных средних
Мi по градациям комплекса от общей средней МΣ:
Сх = Σn (Mi - MΣ)2
Слайд 7Случайная дисперсия (внутригрупповая) равна сумме квадратов центральных отклонений дат (V) от
своих частных средних (Mi) по градациям комплекса:
Сz = Σ (V – Mi)2
Слайд 8Общая дисперсия равна сумме квадратов центральных отклонений дат (V) от общей
средней:
Сy = Σ (V - MΣ)2
Слайд 10Закон аддитивности: в любом дисперсионном комплексе сумма частных дисперсий (факториальной и
случайной) равна общей:
Сх+ Сz= Сy
(78+26)=104
Слайд 14Фактически полученное дисперсионное отношение является величиной случайной, его необходимо сравнить с
табличным (стандартным) значением критерия Фишера Fst для принятого уровня значимости а и чисел степеней свободы. При этом число
степеней свободы для большей дисперсии находят в верхней
строке, а для меньшей - в первом столбце таблицы Фишера.
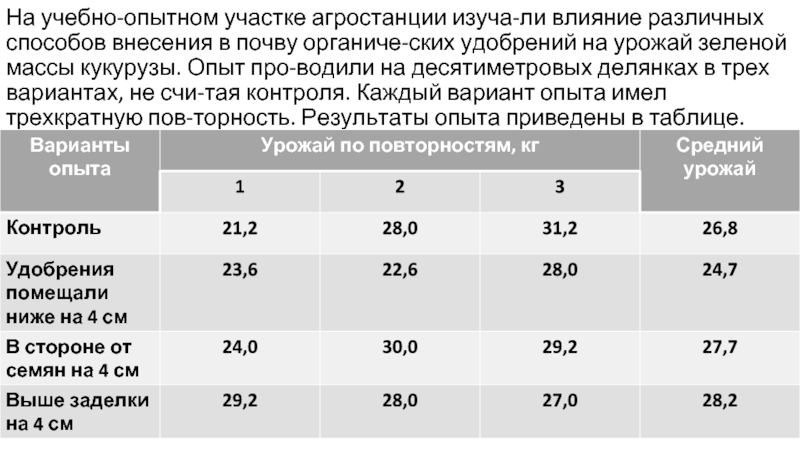
Слайд 15На учебно-опытном участке агростанции изучали влияние различных способов внесения в почву
органических удобрений на урожай зеленой массы кукурузы. Опыт проводили на десятиметровых делянках в трех вариантах, не считая контроля. Каждый вариант опыта имел трехкратную повторность. Результаты опыта приведены в таблице.