- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задача о движении трёх тел презентация
Содержание
- 1. Задача о движении трёх тел
- 2. Задача трёх тел одна из задач небесной механики,
- 3. Математическая формулировка γ - гравитационная постоянная; m -массы тел; q - радиус-векторы, определяющие их положение;
- 4. Появление 1687 г., Исаак Ньютон опубликовал свои
- 5. Частные решения 1772г., Лагранж, мемуар «О задаче
- 6. Общий случай(Вейерштрасс) Пусть дана система произвольного числа
- 7. Приближённое решение Если решение задачи трёх тел
- 8. Ограниченная задача трех тел и точки либрации
- 10. К перечню решений
- 11. К перечню решений
- 12. К перечню решений
Слайд 2Задача трёх тел
одна из задач небесной механики, состоящая в определении относительного движения
трёх тел (материальных точек), взаимодействующих по закону тяготения Ньютона (например, Солнца, Земли и Луны).
Слайд 3Математическая формулировка
γ - гравитационная постоянная;
m -массы тел;
q - радиус-векторы, определяющие их
положение;
Слайд 4Появление
1687 г., Исаак Ньютон опубликовал свои «Принципы» (Математические начала натуральной философии):
первые
шаги в определении и изучении проблемы движений трех массивных тел;
первые шаги в применении своих результатов к лунной теории, движению Луны под действием гравитации Земли и Солнца.
первые шаги в применении своих результатов к лунной теории, движению Луны под действием гравитации Земли и Солнца.
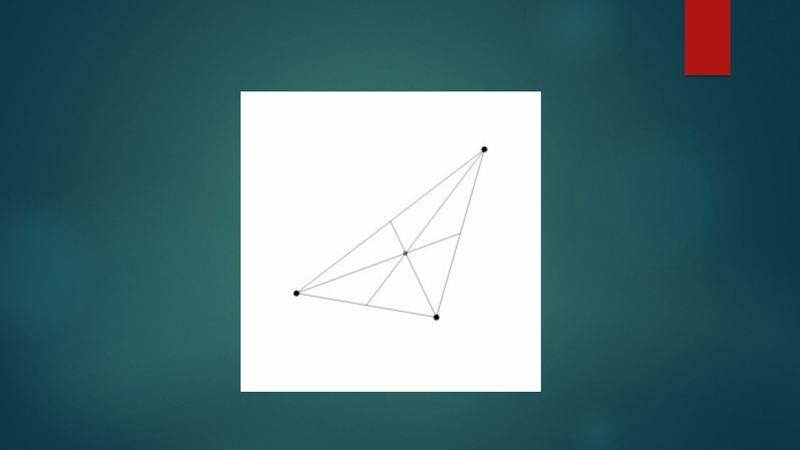
Слайд 5Частные решения
1772г., Лагранж, мемуар «О задаче трех тел»; (изображение)
1767г., Эйлер; (изображение)
1860,1867
гг., Шарль-Эжен Делоне, для системы Солнце–Земля–Луна;
1892–1899 гг., Анри Пуанкаре, существует бесконечно много частных решений;
1911 г., Уильям Дункан Макмиллан, без основания ->1961 г. Кирилл Александрович Ситников(Проблема Ситникова); (изображение)
1970 гг., Брукса, семейство орбит Брукса-Хенона-Хаджидеметриу;
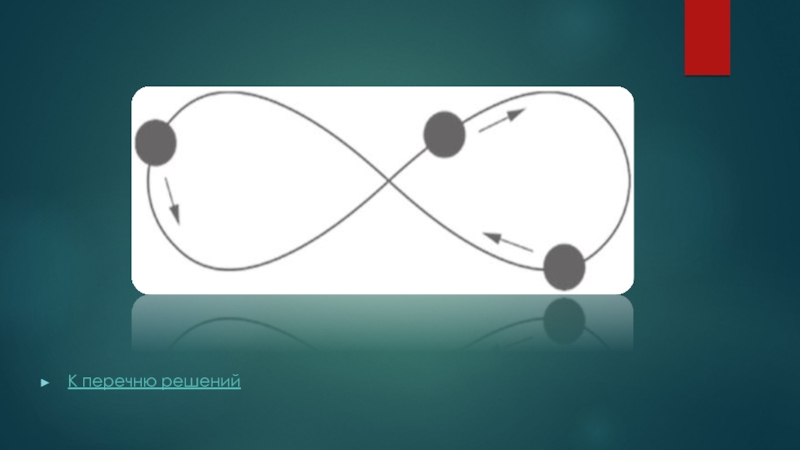
1993 г., Мур, решение, имеющее вид стабильных орбит-восьмерок; (изображение)
2013 г., Милован Шуваков, Велько Дмитрашинович, 13 частных решений;
1892–1899 гг., Анри Пуанкаре, существует бесконечно много частных решений;
1911 г., Уильям Дункан Макмиллан, без основания ->1961 г. Кирилл Александрович Ситников(Проблема Ситникова); (изображение)
1970 гг., Брукса, семейство орбит Брукса-Хенона-Хаджидеметриу;
1993 г., Мур, решение, имеющее вид стабильных орбит-восьмерок; (изображение)
2013 г., Милован Шуваков, Велько Дмитрашинович, 13 частных решений;
Слайд 6Общий случай(Вейерштрасс)
Пусть дана система произвольного числа материальных точек, взаимодействующих по закону
Ньютона. Требуется, в предположении, что не произойдет соударения каких-либо двух точек, представить координаты каждой точки в виде рядов по каким-либо непрерывным функциям времени, равномерно сходящихся для всех действительных значений этой переменной.
Слайд 7Приближённое решение
Если решение задачи трёх тел является аналитической функцией t в
интервале [0,t0] и перестает быть таковым при t = t0, то при t -> t0 - 0 или все расстояния между телами стремятся к нулю (тройное соударение тел), или одно из них стремится к нулю, а остальные два — к конечным пределам (простое соударение тел). (Пенлеве, 1897)
Тройное соударение в задаче трёх тел возможно лишь при условии обращения в нуль момента импульса системы и, следовательно, может иметь место лишь при весьма специальных начальных данных. (Ф. А. Слудский, 1874)
Если момент импульса системы не равен нулю, то существует так называемый регуляризирующий параметр s, через который можно выразить координаты и время голоморфным образом в окрестности вещественной оси s.
Тройное соударение в задаче трёх тел возможно лишь при условии обращения в нуль момента импульса системы и, следовательно, может иметь место лишь при весьма специальных начальных данных. (Ф. А. Слудский, 1874)
Если момент импульса системы не равен нулю, то существует так называемый регуляризирующий параметр s, через который можно выразить координаты и время голоморфным образом в окрестности вещественной оси s.






![Приближённое решениеЕсли решение задачи трёх тел является аналитической функцией t в интервале [0,t0] и перестает](/img/tmb/3/221292/c12616dbb0161dd3bc53c75292093e63-800x.jpg)