- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
XXIV Всероссийская олимпиада школьников по астрономии презентация
Содержание
- 1. XXIV Всероссийская олимпиада школьников по астрономии
- 2. Поезд движется точно на север. При наблюдении
- 3. ϕ = +66.6°; δ = ε = +23.4°. Летнее солнцестояние Север
- 4. Распространенная ошибка: 5° Оценка: не выше 6 баллов.
- 5. Система оценивания: Угловая скорость суточного движения
- 6. На Земле наступило полное лунное затмение. В
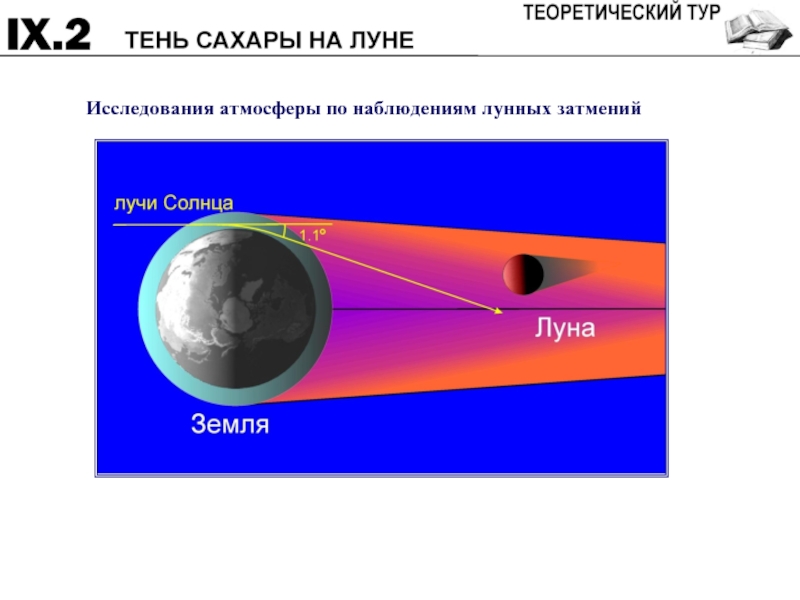
- 7. Исследования атмосферы по наблюдениям лунных затмений
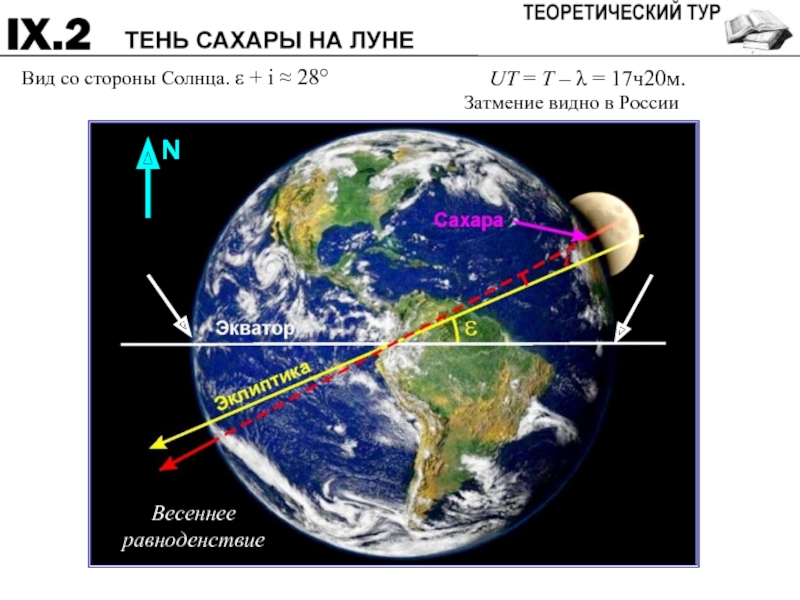
- 8. Вид со стороны Солнца. ε + i
- 9. Система оценивания: Весеннее равноденствие 6 (Осеннее равноденствие) (2)
- 10. В таблице приведены экваториальные координаты Меркурия, Венеры
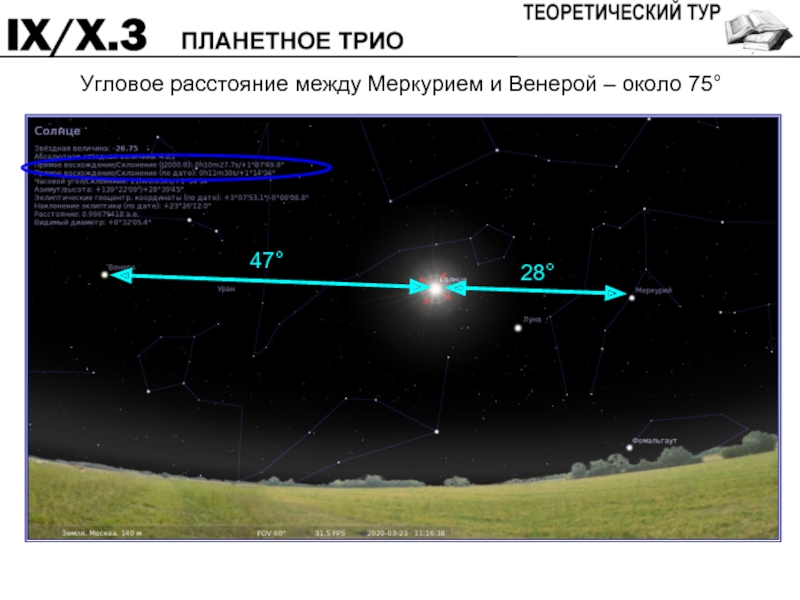
- 11. Угловое расстояние между Меркурием и Венерой – около 75°
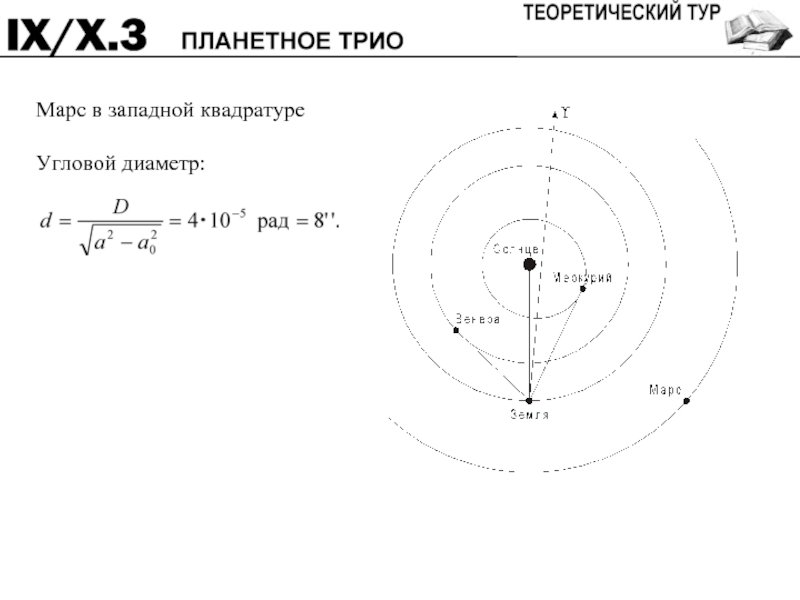
- 12. Марс в западной квадратуре Угловой диаметр:
- 13. Система оценивания: Угловое расстояние между Меркурием
- 14. В начале XVIII века английский астроном Джеймс
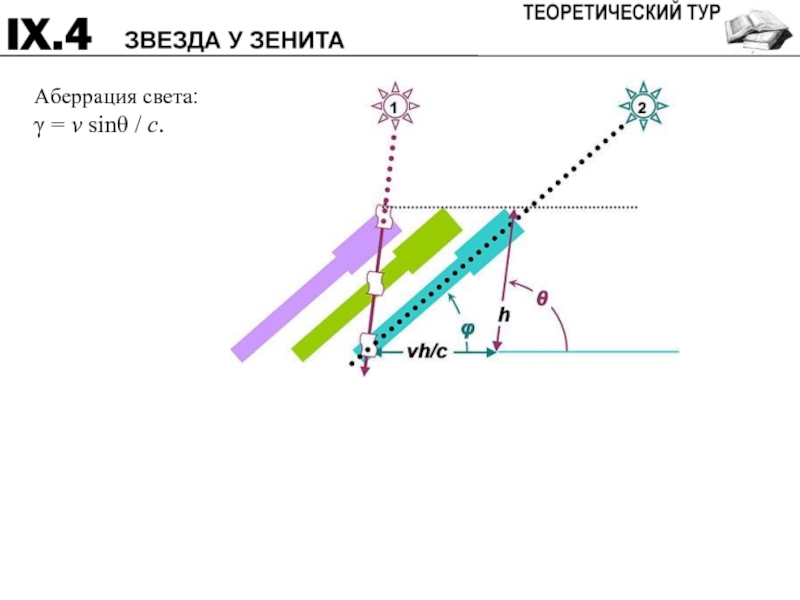
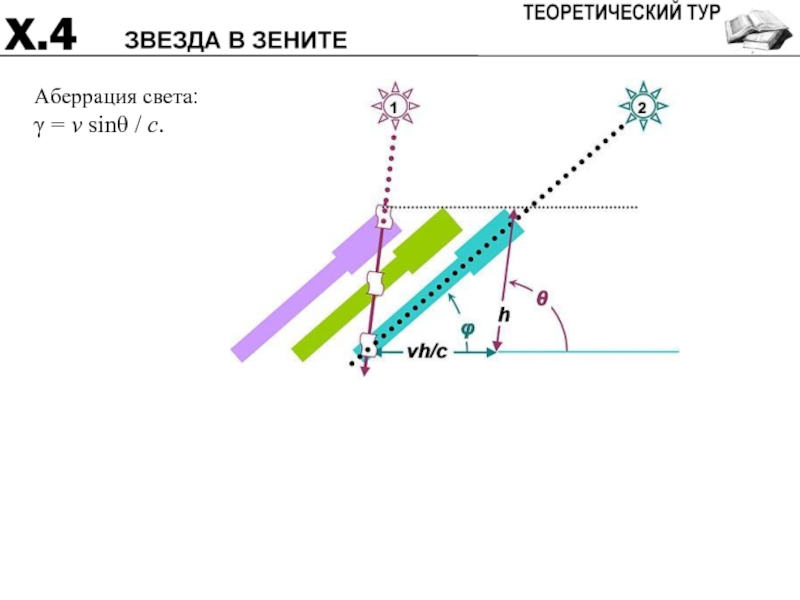
- 15. Аберрация света: γ = v sinθ / c.
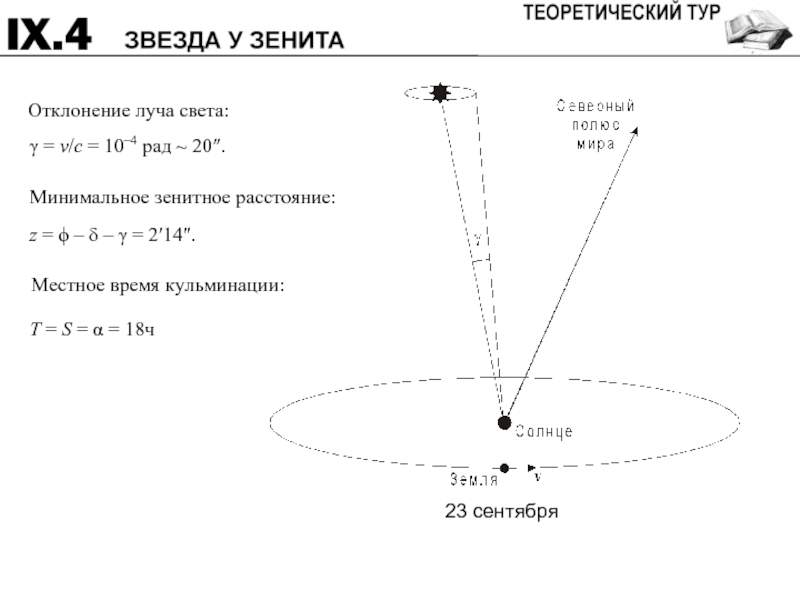
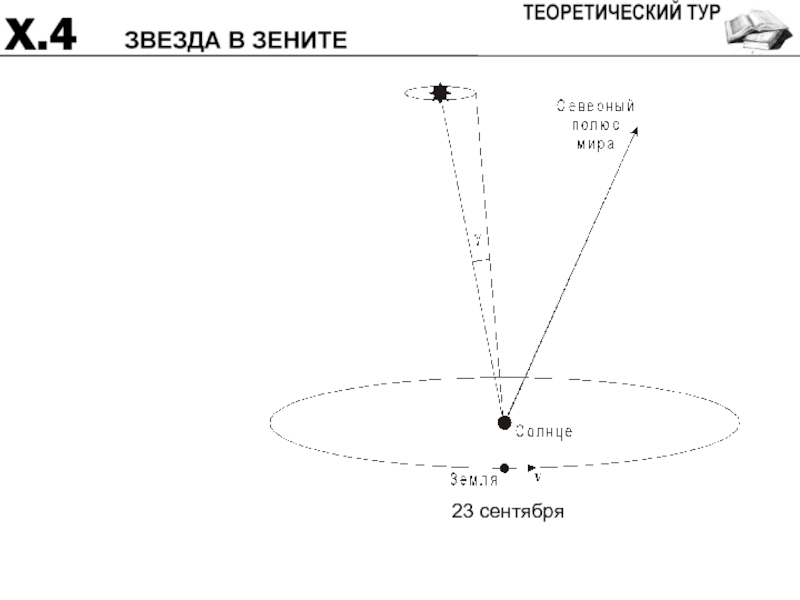
- 17. 23 сентября
- 18. Система оценивания: Направление сдвига 2 Величина сдвига 2
- 19. Штурман космического корабля наблюдает за двойной системой,
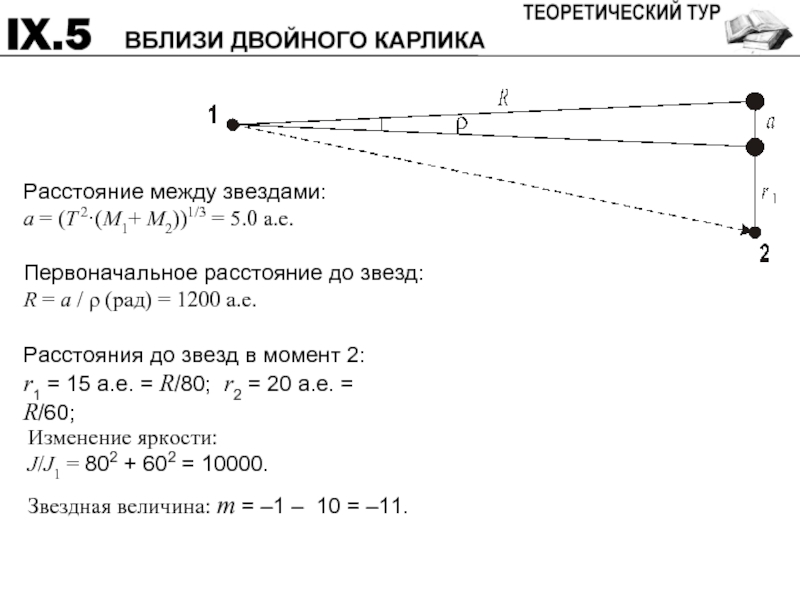
- 20. Расстояние между звездами: a = (T 2·(M1+
- 21. Система оценивания: Расстояние между звездами 4 (Одинарная
- 22. Когда межпланетная станция New Horizons пролетала около
- 24. Система оценивания: Расстояние, соответствующее 1° 4 Скорость
- 25. Океанский корабль движется в сторону севера, пересекая
- 26. Отклонение азимута: A0 = ρ/cosϕ = 80′.
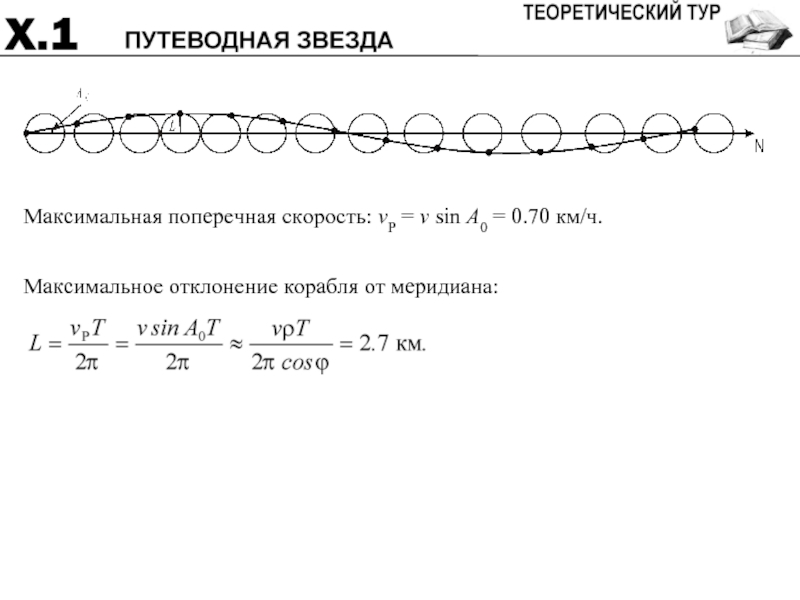
- 27. Максимальная поперечная скорость: vP = v sin A0 = 0.70 км/ч.
- 28. Система оценивания: Отклонение азимута 6 (40’) (0) Поперечная компонента скорости 4 Максимальное отклонение от курса 6 ИТОГО 16
- 29. На стационарной лунной обсерватории будущего проводится изучение
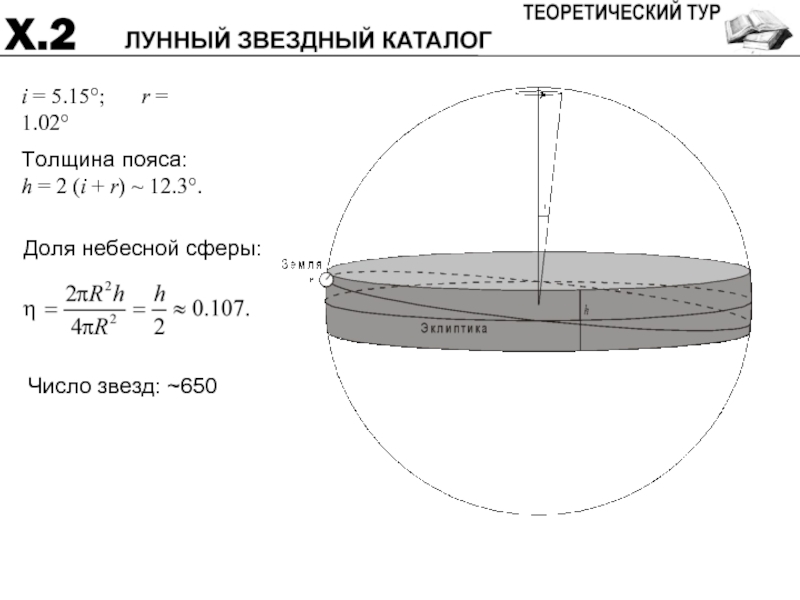
- 30. i = 5.15°; r = 1.02° Толщина пояса:
- 31. Система оценивания: Факторы, влияющие на ширину
- 32. В какой сезон и в какое местное
- 33. Аберрация света: γ = v sinθ / c.
- 35. 23 сентября
- 36. Отличие склонения звезды от широты: Δδ=+13″. Примерные
- 37. Система оценивания: Указание аберрации света 2 Величина
- 38. Враждебные инопланетяне разрушили Луну, превратив ее в
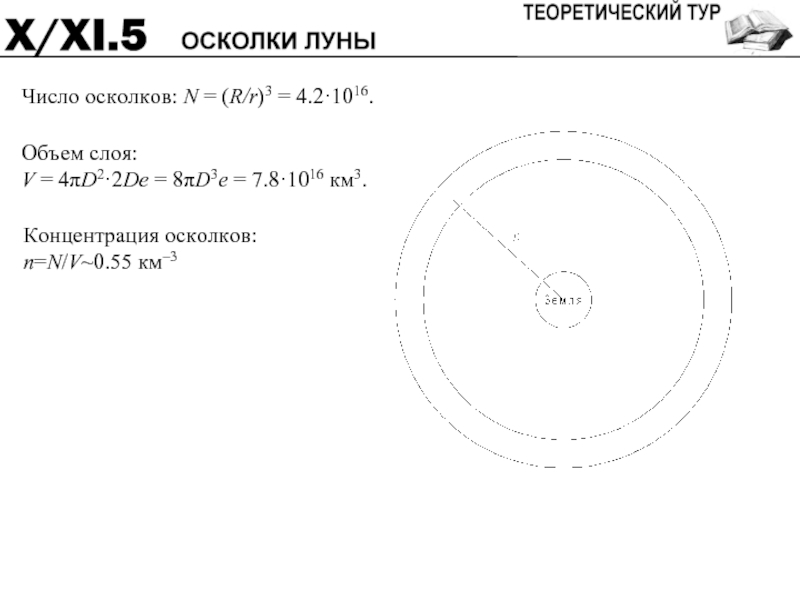
- 39. Число осколков: N = (R/r)3 = 4.2·1016.
- 40. Яркость одного осколка: j = Jr2/R2 (J
- 41. Общее количество задерживаемой энергии Солнца: πD2·J0
- 42. Система оценивания: Концентрация осколков 4 Затенение осколков 2
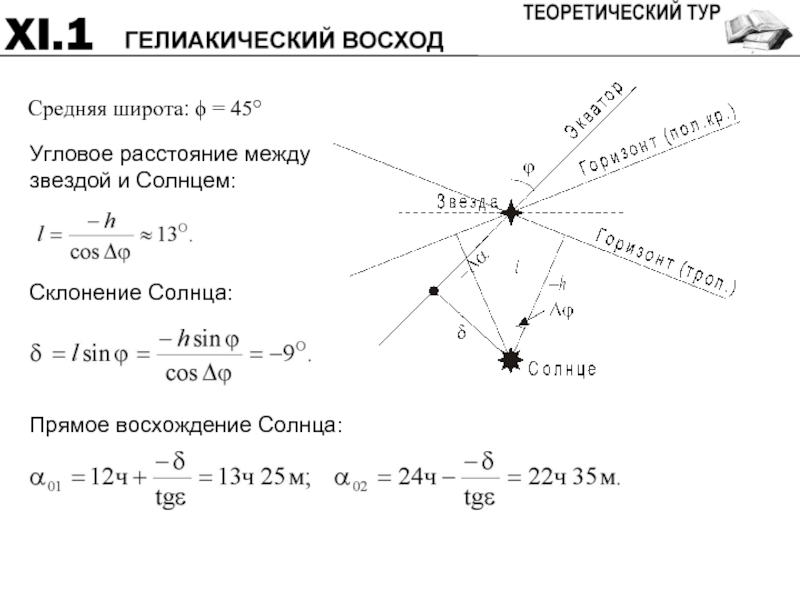
- 43. Гелиакическим восходом звезды называется ее восход на
- 44. Средняя широта: ϕ = 45°
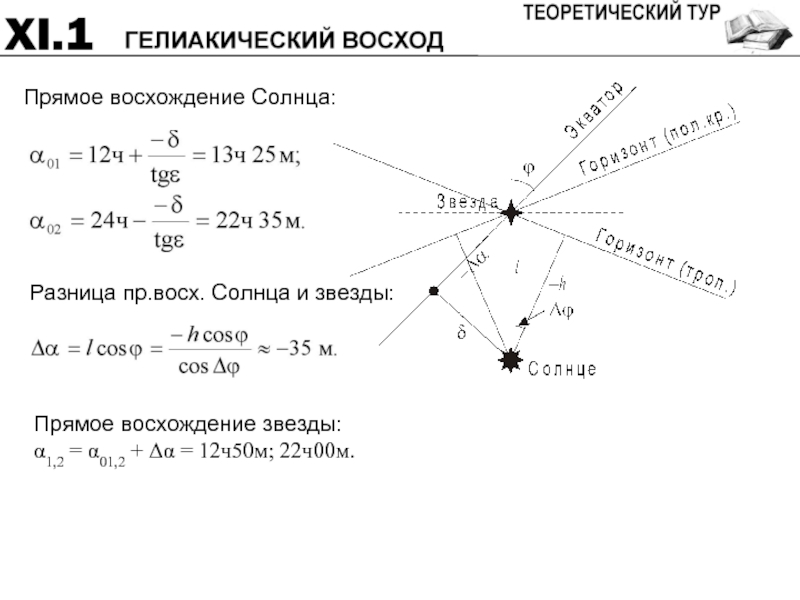
- 45. Прямое восхождение Солнца: Прямое восхождение звезды: α1,2 = α01,2 + Δα = 12ч50м; 22ч00м.
- 46. Система оценивания: Представление о расположении Солнца
- 47. В некоторый момент времени в пункте A
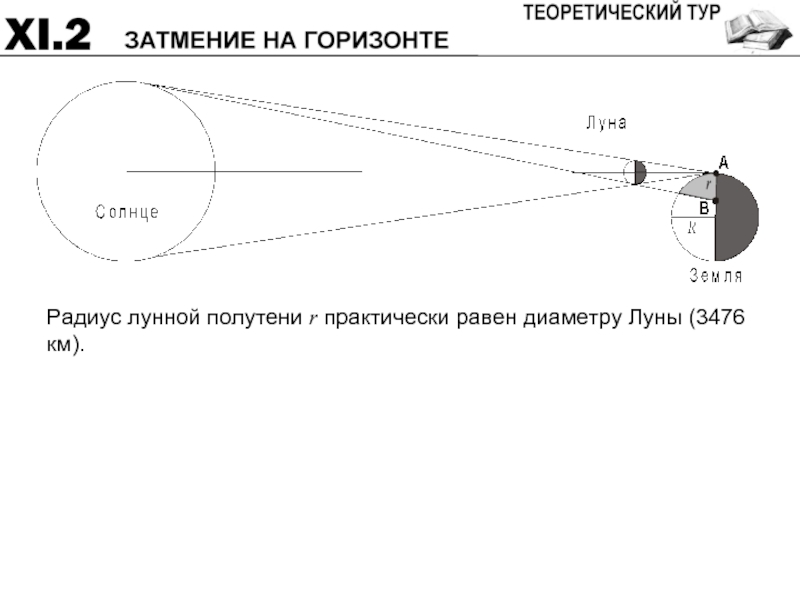
- 48. Радиус лунной полутени r практически равен диаметру Луны (3476 км).
- 50. 3 октября 1986 г.
- 51. Система оценивания: Положение тени и полутени
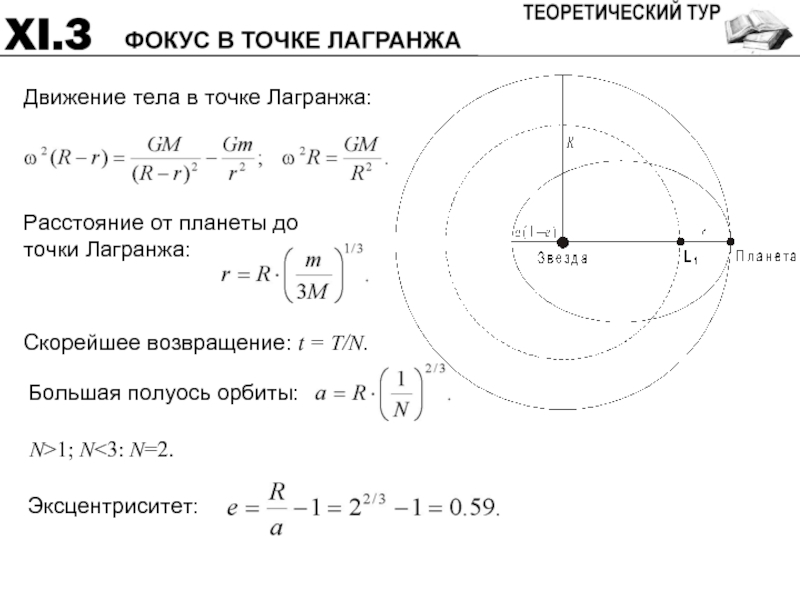
- 52. Планета обращается вокруг звезды с массой M
- 53. Движение тела в точке Лагранжа: Скорейшее возвращение: t = T/N. N>1; N
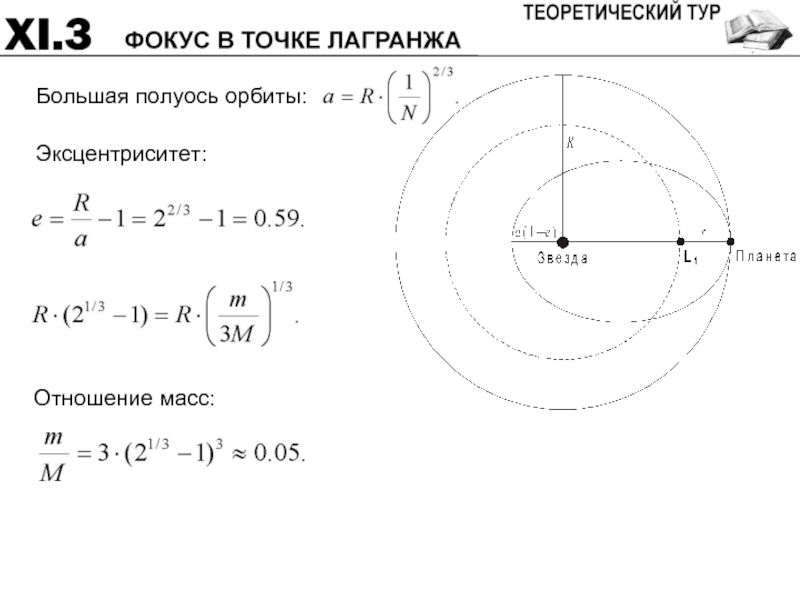
- 54. Эксцентриситет:
- 55. Система оценивания: Расстояние между планетой и
- 56. Суть известного эффекта Пойнтинга-Робертсона состоит в тормозящем
- 57. Эффективная масса Солнца: M’=0.92M.
- 58. Полная энергия частицы:
- 59. Система оценивания: Сравнение сил гравитации и
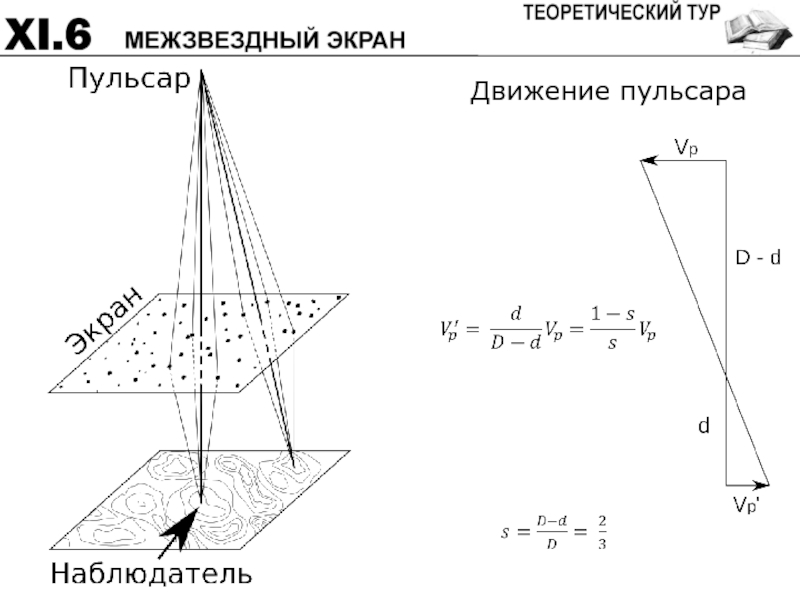
- 60. Излучение пульсара на пути к Земле проходит
- 61. Движение пульсара
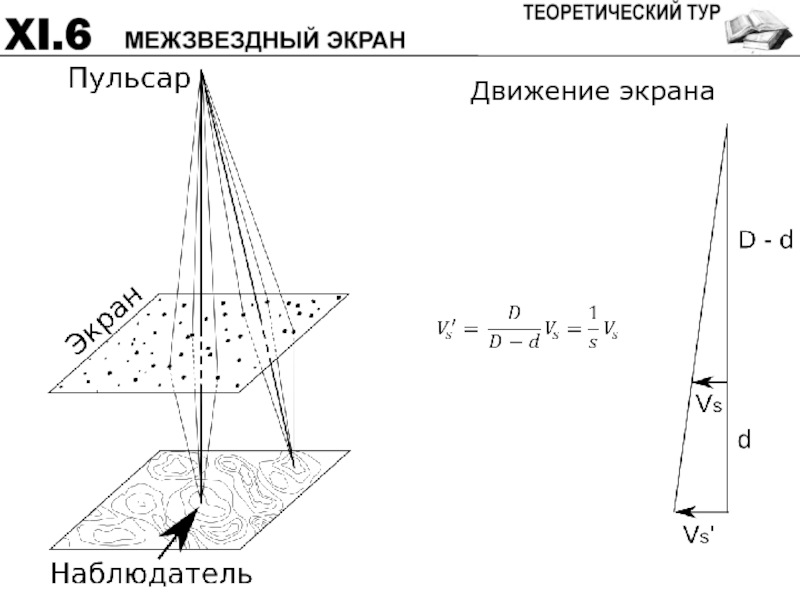
- 62. Движение экрана
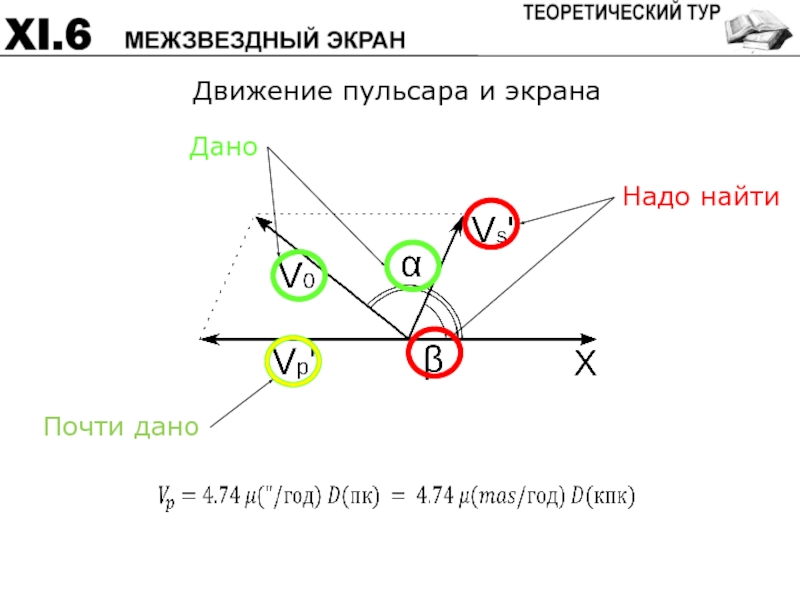
- 63. Движение пульсара и экрана Дано Надо найти Почти дано
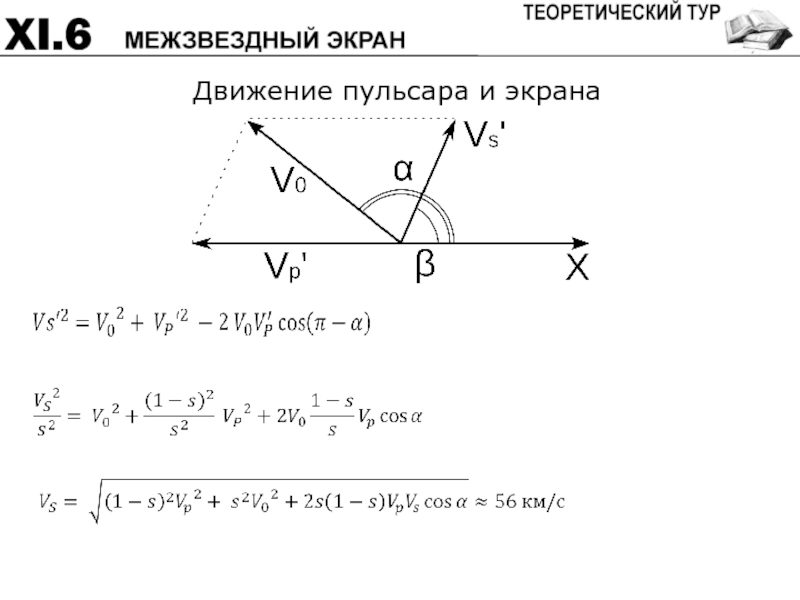
- 64. Движение пульсара и экрана
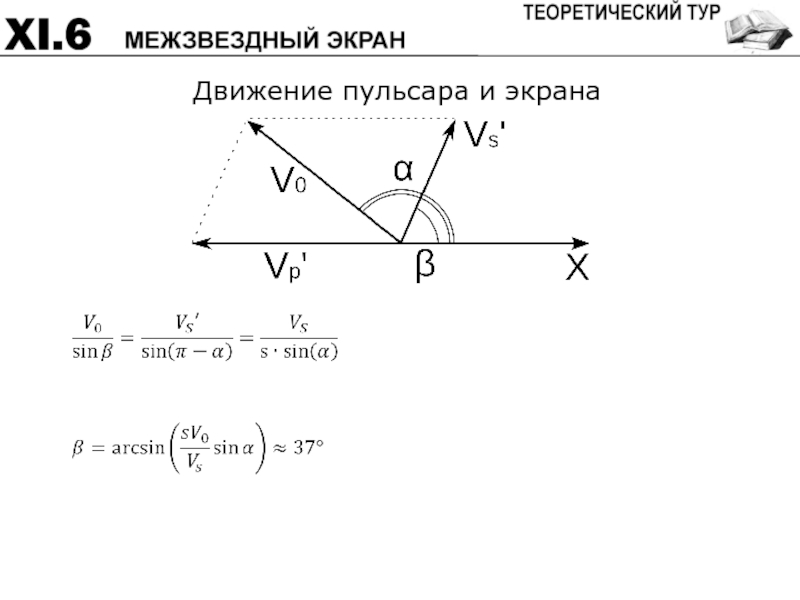
- 65. Движение пульсара и экрана
- 66. Система оценивания: Правильная геометрическая модель 4
Слайд 1Министерство образования и науки Российской Федерации
Академия повышения квалификации и профессиональной
переподготовки
XXIV Всероссийская олимпиада школьников по астрономии
Заключительный этап
г. Смоленск, 20-26 марта 2017 г.
Теоретический тур
Слайд 2Поезд движется точно на север. При наблюдении из этого поезда в
Слайд 5Система оценивания:
Угловая скорость суточного движения Солнца 8
(Не учтен cos ε) (6)
Анализ вертикального движения
Скорость поезда 4
ИТОГО 16
Слайд 6На Земле наступило полное лунное затмение. В ходе его наблюдений в
Слайд 8Вид со стороны Солнца. ε + i ≈ 28°
UT = T
Весеннее
равноденствие
Затмение видно в России
N
Слайд 9Система оценивания:
Весеннее равноденствие 6
(Осеннее равноденствие) (2)
Заход Солнца в Сахаре 6
(Восход) (2)
Всемирное время 2
Видимость затмения в России 2
(обосновано!)
ИТОГО 16
Слайд 10В таблице приведены экваториальные координаты Меркурия, Венеры и Марса на Земле
Слайд 13Система оценивания:
Угловое расстояние между Меркурием и Венерой 4
Противоположные элонгации 4
Положение Солнца 2
Квадратура Марса 2
(либо его
Угловой диаметр Марса 4
ИТОГО 16
Слайд 14В начале XVIII века английский астроном Джеймс Бредли пытался определить параллакс
Слайд 18Система оценивания:
Направление сдвига 2
Величина сдвига 2
Сезон 4
Местное время 4
Минимальное зенитное расстояние 4
ИТОГО 16
Ошибочное направление ≤10
Игнорирование явлением аберрации ≤4
Слайд 19Штурман космического корабля наблюдает за двойной системой, состоящей их двух одинаковых
Слайд 20Расстояние между звездами:
a = (T 2·(M1+ M2))1/3 = 5.0 а.е.
Первоначальное
R = a / ρ (рад) = 1200 а.е.
Расстояния до звезд в момент 2:
r1 = 15 а.е. = R/80; r2 = 20 а.е. = R/60;
Изменение яркости:
J/J1 = 802 + 602 = 10000.
Звездная величина: m = –1 – 10 = –11.
Слайд 21Система оценивания:
Расстояние между звездами 4
(Одинарная масса) (0)
Расстояние до звезд в первый момент 2
Расстояние до
Звездная величина 6
ИТОГО 16
Слайд 22Когда межпланетная станция New Horizons пролетала около Плутона (радиус 1190 км)
Слайд 24Система оценивания:
Расстояние, соответствующее 1° 4
Скорость аппарата относительно Плутона 4
(Ошибка в 2 раза) (0)
(Хорда, правильные
Аппарат покинет Солнечную систему 2
Радиальное направление скорости 2
Время перелета к 2014 MU69 4
ИТОГО 16
Слайд 25Океанский корабль движется в сторону севера, пересекая параллель +60° с.ш. Капитан
Слайд 28Система оценивания:
Отклонение азимута 6
(40’) (0)
Поперечная компонента скорости 4
Максимальное отклонение от курса 6
ИТОГО 16
Слайд 29На стационарной лунной обсерватории будущего проводится изучение атмосферы Земли на основе
Слайд 31Система оценивания:
Факторы, влияющие на ширину области 10
(Прецессия орбиты Луны) (6)
(Видимые размеры Земли) (4)
(Величина либрации
(Параллакс, либрации, 2*0.03°) (=)
(Параллакс, полный, 2*0.25°) (-4)
(Ошибка в 2 раза для каждого фактора) (-2)
Доля небесной сферы 4
Число звезд 2
ИТОГО 16
Слайд 32В какой сезон и в какое местное (среднее солнечное) время звезда
Слайд 36Отличие склонения звезды
от широты: Δδ=+13″.
Примерные даты:
30 января (S0 = 8ч
Местное время:
T = α – S = 9м20м или 2ч40м.
Слайд 37Система оценивания:
Указание аберрации света 2
Величина сдвига 2
Направление сдвига 4
Сезон 4 (2+2)
Местное время 4 (2+2)
ИТОГО 16
Игнорирование явлением аберрации 2
Слайд 38Враждебные инопланетяне разрушили Луну, превратив ее в огромное количество шарообразных осколков
Слайд 39Число осколков: N = (R/r)3 = 4.2·1016.
Объем слоя:
V = 4πD2·2De
Концентрация осколков:
n=N/V~0.55 км–3
Слайд 40Яркость одного осколка: j = Jr2/R2 (J – яркость Луны в
Суммарная яркость (N/2) осколков:
J = (N/2) j = JR/2r.
Звездная величина фона неба:
m = m0 – 2.5 lg (JR / 2r) =
= m0 – 13.1 ≈ –23.6.
Как дневное небо на Земле???
Не может быть!!!
Осколки затеняют друг друга
Слайд 42Система оценивания:
Концентрация осколков 4
Затенение осколков 2
Модель определения звездной величины 6
Расчет звездной величины 4
ИТОГО 16
Оптически тонкий случай ≤8
Оптически
Слайд 43Гелиакическим восходом звезды называется ее восход на фоне утренней зари, при
Слайд 46Система оценивания:
Представление о расположении Солнца и звезды 4
Склонение Солнца 2
Прямое восхождение Солнца 4 (2+2)
Разность
Прямое восхождение звезды 4 (2+2)
ИТОГО 16
Слайд 47В некоторый момент времени в пункте A на Земле наблюдается полное
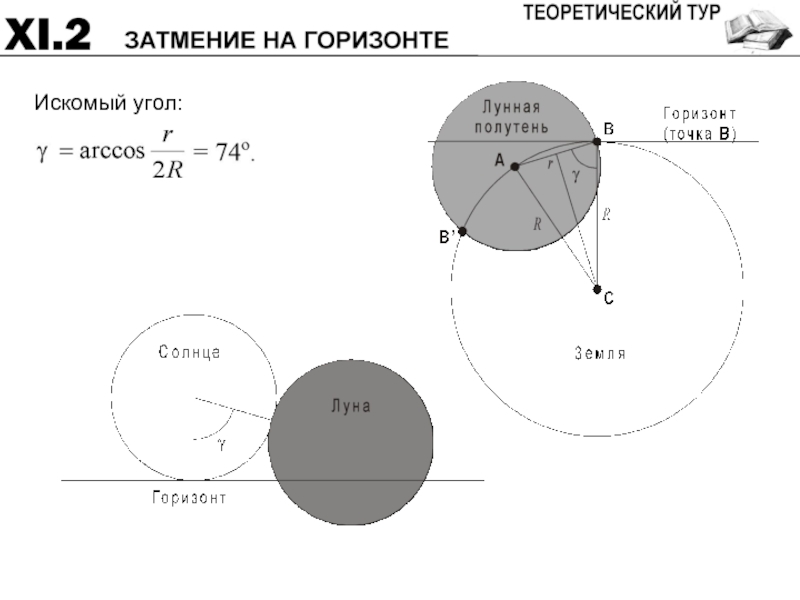
Слайд 51Система оценивания:
Положение тени и полутени на Земле 4
Вывод об угле γ 4
Размер полутени
Окончательный вывод 4
ИТОГО 16
Слайд 52Планета обращается вокруг звезды с массой M по круговой орбите с
Слайд 55Система оценивания:
Расстояние между планетой и точкой Лагранжа 6
Условие скорейшего возвращения 4
Отношение масс 6
ИТОГО 16
Слайд 56Суть известного эффекта Пойнтинга-Робертсона состоит в тормозящем действии боковых солнечных фотонов,
Слайд 59Система оценивания:
Сравнение сил гравитации и св.давления 2
(либо вычисление эффективной массы Солнца)
Выражение для
Изменение радиуса орбиты 8
(Изменение кинетической энергии, ошибка в знаке) (0)
ИТОГО 16
Слайд 60Излучение пульсара на пути к Земле проходит через тонкий рассеивающий слой
Слайд 66Система оценивания:
Правильная геометрическая модель 4
Вычисление тангенциальной скорости пульсара 2
Формула для связи скоростей экрана,
и интерференционной картины
(в векторах или в проекциях) 2
Формулы для вычисления искомых величин β и Vs 4
(По 2 балла за куждую)
Вычисление искомых величин β и Vs 4
(По 2 балла за куждую)
ИТОГО 16