- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Силы и моменты, действующие на ракету в полёте презентация
Содержание
- 1. Силы и моменты, действующие на ракету в полёте
- 2. Вопросы занятия: 1-ый вопрос: Аэродинамическая компоновка
- 3. 1-ый вопрос: Аэродинамическая компоновка ЗУР.
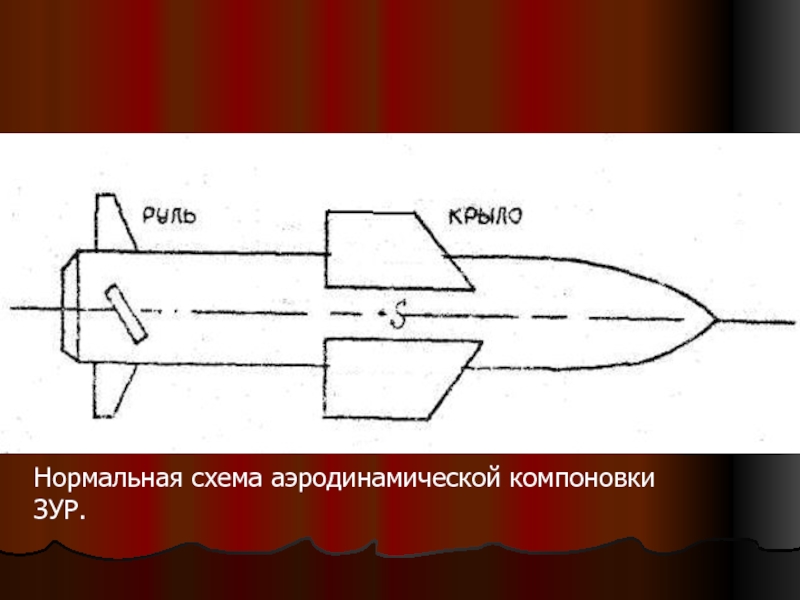
- 4. Нормальная схема аэродинамической компоновки ЗУР.
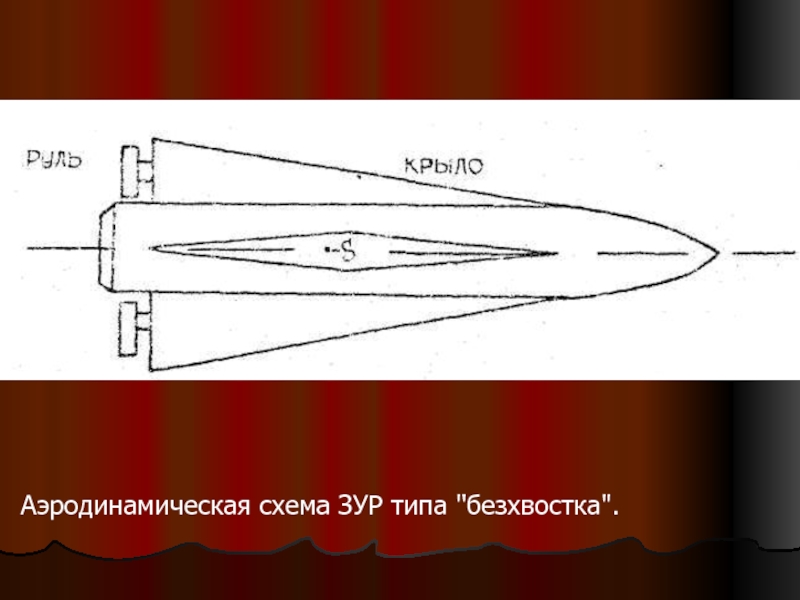
- 5. Аэродинамическая схема ЗУР типа "безхвостка".
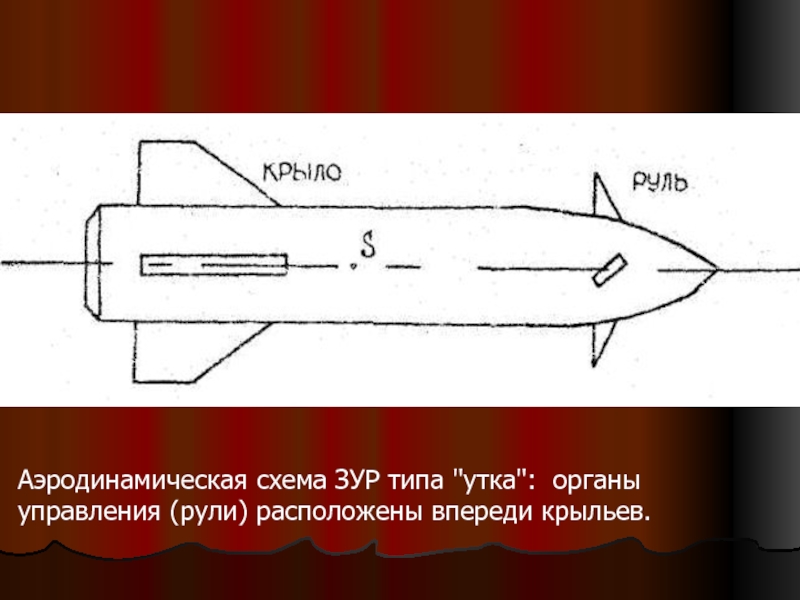
- 6. Аэродинамическая схема ЗУР типа "утка": органы управления (рули) расположены впереди крыльев.
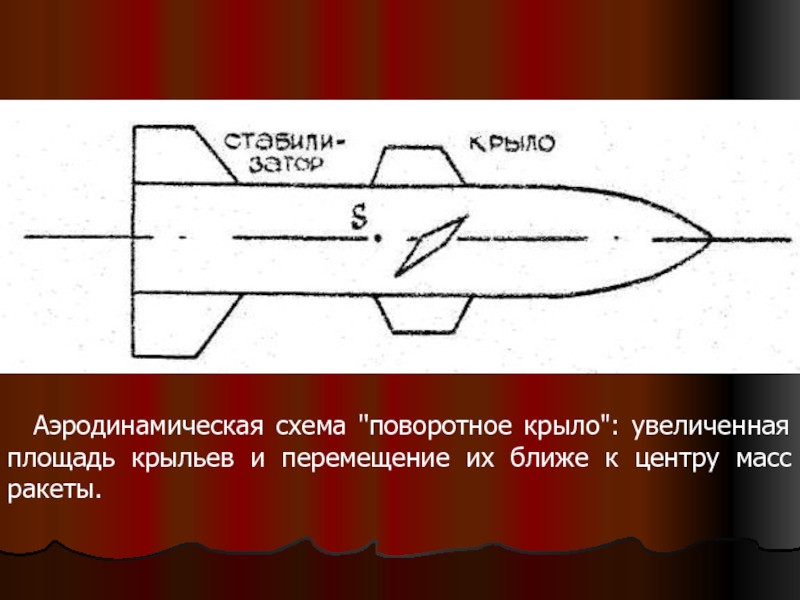
- 7. Аэродинамическая схема "поворотное крыло": увеличенная
- 8. 2-ой вопрос. Аэродинамические моменты, действующие на ракету
- 9. mR - безразмерный аэродинамический коэффициент,
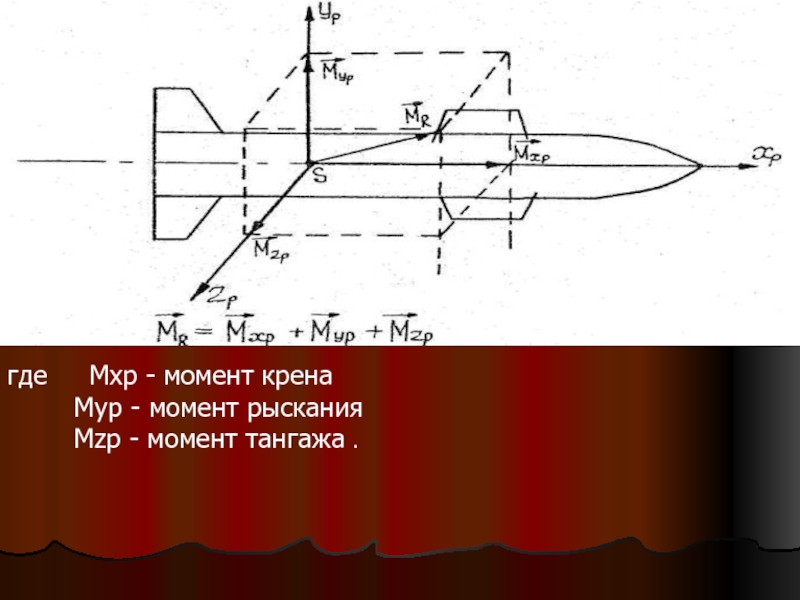
- 10. где Мхр - момент крена
- 11. Управляющие, стабилизирующие, и тушащие
- 12. Ракеты, которые под действием
- 13. Управляющий момент тангажа Mzpу
- 14. Под воздействием управляющего момента
- 15. Тушащий (демпфирующий) момент тангажа
- 16. Величина тушащего момента пропорциональна угловой скорости ωzр
- 17. 3-ий вопрос: Перегрузки, создаваемые на ракете.
- 18. Кинематическая траектория ракеты представляет
- 19. Число, полученное от деления
- 20. nтр= nk +nb + nф
- 21. 4-ый вопрос: Силы, действующие на ракету в
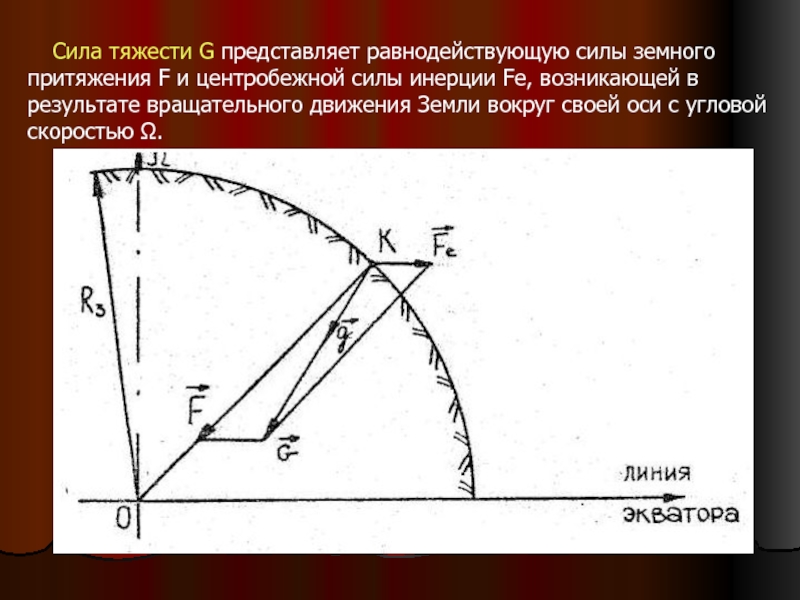
- 22. Сила тяжести G представляет равнодействующую
- 23. При условии Fе
- 24. Сила тяги двигателя P - представляет
- 25. Для ракетного двигателя сила тяги P определяется
- 26. Полная аэродинамическая сила R -
- 27. Величина полной аэродинамической силы R
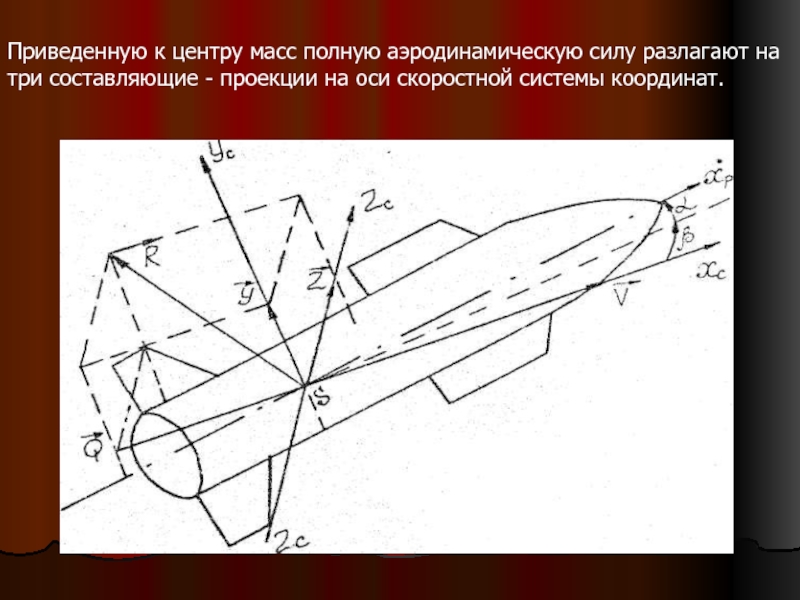
- 28. Приведенную к центру масс полную аэродинамическую силу
- 29. Проекция полной аэродинамической силы на
- 30. Лобовое сопротивление Q→ действует в
- 31. Подъемная Y и
- 32. Вводя обозначение, где Уα α -
Слайд 1Тема № 2. «Зенитная управляемая ракета 9М39.»
Занятие № 3. «Силы и
Слайд 2Вопросы занятия:
1-ый вопрос: Аэродинамическая компоновка ЗУР.
2 - ой вопрос: Аэродинамические
3 – ий вопрос: Перегрузки, создаваемые на ракете.
4-ый вопрос: Силы, действующие на ракету в полёте.
Слайд 31-ый вопрос: Аэродинамическая компоновка ЗУР.
Под аэродинамической компоновкой ЗУР
Аэродинамическая схема ЗУР в общем случае включает в себя корпус, крылья, органы управления и стабилизации.
Аэродинамически симметричной называется ракета, при вращении которой вокруг продольной оси, при заданной ориентации её относительно набегающего воздушного потока, аэродинамические силы и моменты не меняются как по величине, так и по направлению.
В зависимости от взаимного расположения рулей и крыльев на корпусе ракеты, аэродинамическая компоновка её может быть выполнена:
- по нормальной схеме;
- по схеме «безхвостка»;
- по схеме «утка»;
- по схеме с поворотным крылом.
Слайд 6Аэродинамическая схема ЗУР типа "утка": органы управления (рули) расположены впереди крыльев.
Слайд 7 Аэродинамическая схема "поворотное крыло": увеличенная площадь крыльев и перемещение
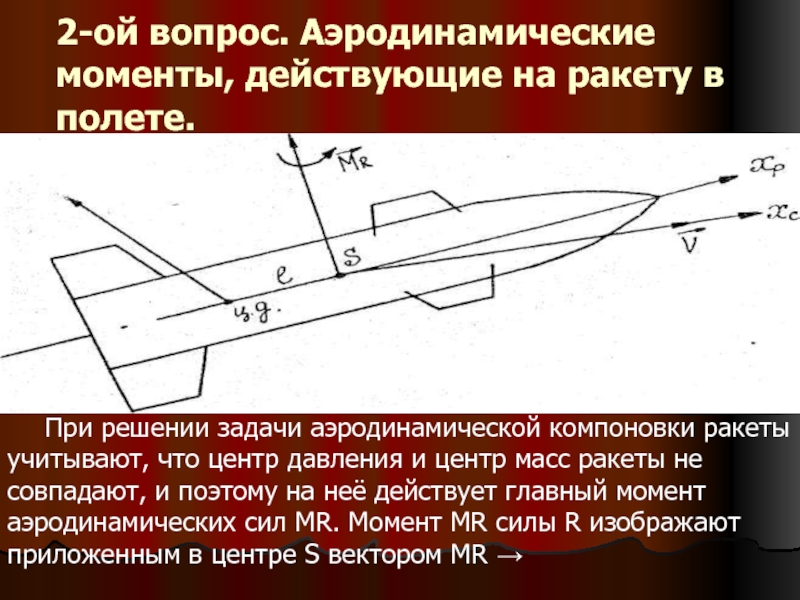
Слайд 82-ой вопрос. Аэродинамические моменты, действующие на ракету в полете.
Слайд 9 mR - безразмерный аэродинамический коэффициент, зависящий от формы ракеты,
ba - средняя аэродинамическая хорда крыла.
q – величина скоростного напора.
Главный момент аэродинамических сил поворачивает ракету вокруг её центра масс.
При изучении вращения ракеты вокруг центра масс главный момент аэродинамических сил принято раскладывать на три составляющие по осям связанной системы координат SXpYpZp (см.рис)
Слайд 11 Управляющие, стабилизирующие, и тушащие моменты крена, рыскания и
Стабилизирующий момент тангажа Мzpcт возникает при отклонении продольной оси ракеты в вертикальной плоскости от направления вектора скорости V , т.е. при возникновении угла атаки α (см. рис.) Он создается составляющей подъемной силы Уα α.
Слайд 12 Ракеты, которые под действием стабилизирующего момента возвращаются в
Величина стабилизирующего момента тангажа пропорциональна углу атаки α.
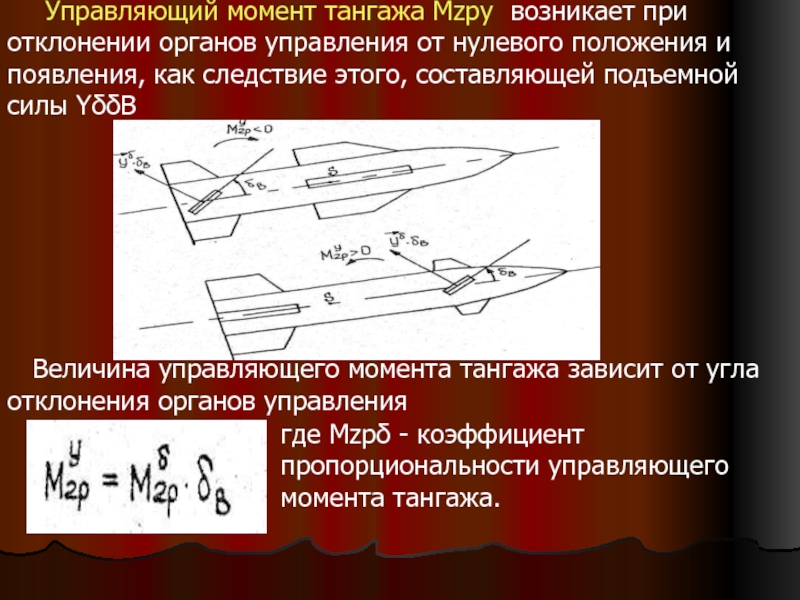
Слайд 13 Управляющий момент тангажа Mzpу возникает при отклонении органов
Величина управляющего момента тангажа зависит от угла отклонения органов управления
где Mzpδ - коэффициент пропорциональности управляющего момента тангажа.
Слайд 14 Под воздействием управляющего момента тангажа ракета поворачивается вокруг
который действует в противоположном направлении, то ракета непрерывно вращалась бы вокруг оси SZp. При условии равенства стабилизирующего момента управляющему моменту (Мzpст = Мzpу), вращение ракеты прекратится и установится угол атаки, который будет зависеть от угла поворота органов управления.
Слайд 15 Тушащий (демпфирующий) момент тангажа МzрT обусловлен возникновением дополнительных
При вращении ракеты дополнительные аэродинамические силы в её передней части будут направлены вниз, а в хвостовой части вверх. Поэтому момент, обусловленный угловой скоростью вращения ракеты вокруг оси SZp, будет иметь направление противоположное направлению угловой скорости ωzр, Этот момент препятствует вращению ракеты и поэтому называется тушащим (или демпфирующим) моментом тангажа, знаки тушащего момента и угловой скорости противоположны.
Слайд 16Величина тушащего момента пропорциональна угловой скорости ωzр =V.
ωzp - угловая скорость вращения ракеты относительно поперечной оси SZp
Величины аэродинамических моментов тангажа зависят от скоростного напора, а следовательно, с увеличением высоты они уменьшаются. То же относится и к аэродинамическим моментам крена и рыскания.
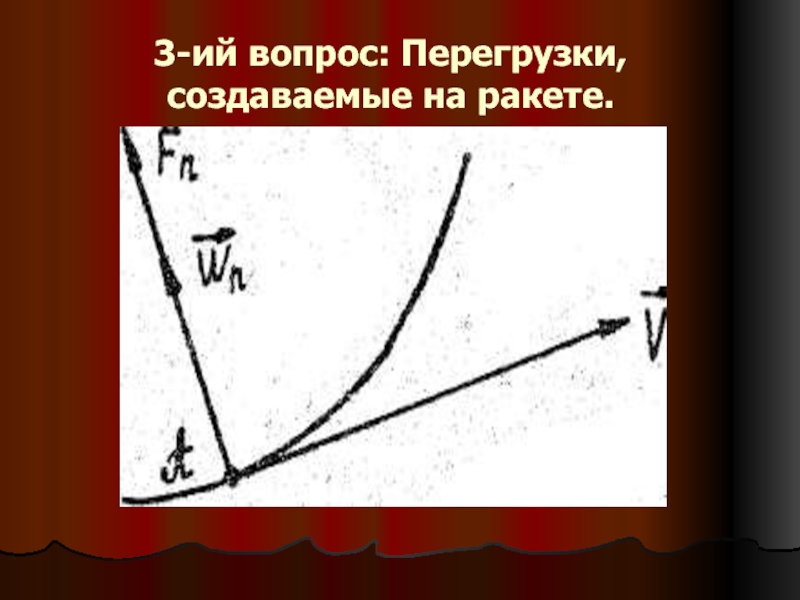
Слайд 18 Кинематическая траектория ракеты представляет собой некоторую кривую линию,
Согласно третьему закону Ньютона
, где
- масса ракеты,
Fn - сумма проекций всех сил на ось Yc
Wn- нормальное ускорение ракеты.
Силы составляющие Fn можно измерять не в Ньютонах, а принять за единицу измерения вес ракеты G, т.е. силу, эффект действия которой - ускорение g - известен. В таком случае, разделив значение, силы Fn, на вес ракеты G, можно сказать, сколько единиц веса содержится в ней и какое ускорение в величинах g она создает.
Fn/G = m ⋅ Wn / m ⋅ g = Wn/g = n
Слайд 19 Число, полученное от деления величины силы, действующей на
Т.о. перегрузка есть число, показывающее во сколько раз сила, действующая на ракету в полете больше веса ракеты. Перегрузки, действующие вдоль осей SУс и SZс характеризуют быстроту изменения направления полета ракеты в вертикальной или горизонтальной (наклонной) плоскостях и являются нормальными по отношению к траектории полета ракеты перегрузками. Они зависят в основном от величины подъемной и боковой сил.
Отношение переменной силы, необходимой для движения ракеты по кинематической траектории к весу ракеты принято называть нормальной кинематической перегрузкой, nк.
Нормальные кинематические перегрузки, которые должна развивать ракета для движения по траектории метода наведения с заданной точностью называются потребными перегрузками, nтр.
Потребные перегрузки определят требования к маневренным свойствам ракеты, т.е. к её способности осуществлять криволинейные траектории.
Слайд 20nтр= nk +nb + nф
nk - кинематические
nb - перегрузки веса
nф - флюктуационные, случайные перегрузки.
Реальная ракета обладает ограниченной маневренностью. Нормальные силы, изменяющие направление движения ракеты, являются аэродинамическими силами. При данной аэродинамической компановке ракеты, наибольшая нормальная аэродинамическая сила может быть получена при выдаче на рули ракеты максимальной команды управления.
Параметры перегрузки, возникающие на ракете при максимальной команде управления, называются располагаемыми перегрузками, np.
Для наведения ракеты на цель с заданной точностью, располагаемые перегрузки всегда должны быть больше требуемых (потребных):
Слайд 214-ый вопрос: Силы, действующие на ракету в полёте.
При
Слайд 22 Сила тяжести G представляет равнодействующую силы земного притяжения F
Слайд 23 При условии Fе
Сила тяжести G рассчитывается по формуле
где
G0 - все ракеты перед стартом,
G1 - вес стартовых ускорителей,
Gc(t) - секундный весовой расход топлива,
t - текущее время.
Слайд 24Сила тяги двигателя P - представляет собой равнодействующую сил реакций
В зенитных ракетах наиболее широко используются два типа двигателей - воздушно-реактивные и ракетные.
В воздушно-реактивных двигателях для создания газовой струи в качестве окислителя используется атмосферный воздух, поступающий в камеру сгорания через воздухозаборник.
В ракетных двигателях сгорание топлива происходит без участия воздуха.
Величина силы тяги воздушно-реактивного двигателя может быть рассчитана по формуле:
где
Gт - секундный расход топлива, кг/сек,
Gb - секундный расход воздуха, кг/сек
Sа - площадь сечения сопла двигателя, м2,
Wa - относительная скорость истечения газов из сопла двигателя, м/сек,
V - скорость ракеты, м/сек,
Pa - давление газов на срезе сопла, (кг*см)/м2
Po - атмосферное давление на высоте полёта ракеты, кг*сек/м2.
Слайд 25Для ракетного двигателя сила тяги P определяется по формуле :
При изучении движения ЗУР принято, что сила тяги приложена к центру масс и направлена вдоль продольной оси ракеты, хотя в действительности имеют место отклонения линии действия силы Р от продольной оси ракеты.
Слайд 26 Полная аэродинамическая сила R - это сила, возникающая в
Слайд 27 Величина полной аэродинамической силы R зависит от формы и
Величина полной аэродинамической силы определяется известной из аэродинамики формулой
R=Cr× q× Skp
Cr- безразмерный аэродинамический коэффициент,
q- скоростной напор, равный q =ρV2/2 (кг/м2 )
ρ - массовая плотность воздуха кг*сек2/м4
Skp - характерная площадь крыла, м2.
С увеличением высоты полета уменьшается и величина полной аэродинамической силы.
Так как величина, направление и точка приведения полной аэродинамической сипы в процессе полёта изменяются, то с целью удобства изучения влияния этой силы на движение ракеты её переносят в центр масс и раскладывают на составляющие по осям скоростной системы координат.
Слайд 28Приведенную к центру масс полную аэродинамическую силу разлагают на три составляющие
Слайд 29 Проекция полной аэродинамической силы на ось SXc направлена в
R = Q + Y + Z
где: Cx, Сy, Cz - коэффициенты аэродинамических сил лобового сопротивления, подъемной силы и боковой силы.
Слайд 30 Лобовое сопротивление Q→ действует в направлении уменьшения скорости ракеты.
Величина силы лобового сопротивления существенно зависит от коэффициента Сx,который в свою очередь зависит, в основном, от форм и размеров ракеты, числа М =V/a, углов атаки α и скольжения β и углов отклонения органов управления δ, и определяется экспериментально.
С увеличением высоты полета величина лобового сопротивления падает.
Слайд 31 Подъемная Y и боковая Z силы лежат
Су=Суα α + Cyσ δв
где Суα , Cyσ – коэффициенты пропорциональности, характеризующие приращение коэффициента подъемной силы Су, при изменении соответственно угла атаки α и угла отклонения органа управления δв по высоте на единицу и зависящие от числа М. Формулу для подъемной силы можно записать в виде:
Слайд 32 Вводя обозначение, где Уα α - составляющая подъемной силы от
Yδ δв - составляющая подъемной силы от δв.
При одинаковых условиях полёта ракеты типа "утка" и "поворотное крыло", у которых органы управления расположены впереди центра масс, при одном и том же угле поворота органов управления δв могут создать большую величину подъемной силы Y, чем ракета нормальной аэродинамической схемы.